Oct 14, 16 · {–1, 1, 2198, , , , , , , , , , , ,P E is the classical Euler collapse load, P E =π 2 EI/l 2, l being the effective length, Figure 450 Figure 450 The designer must therefore decide first what initial bow is likely;Value (shown in Blue ) when ideal conditions are approximated) Dr ME Haque, PE LRFD Axially Loaded Compression Members Page 4 of 4 AISC Table B41a (AISC Steel Manual 14th Ed
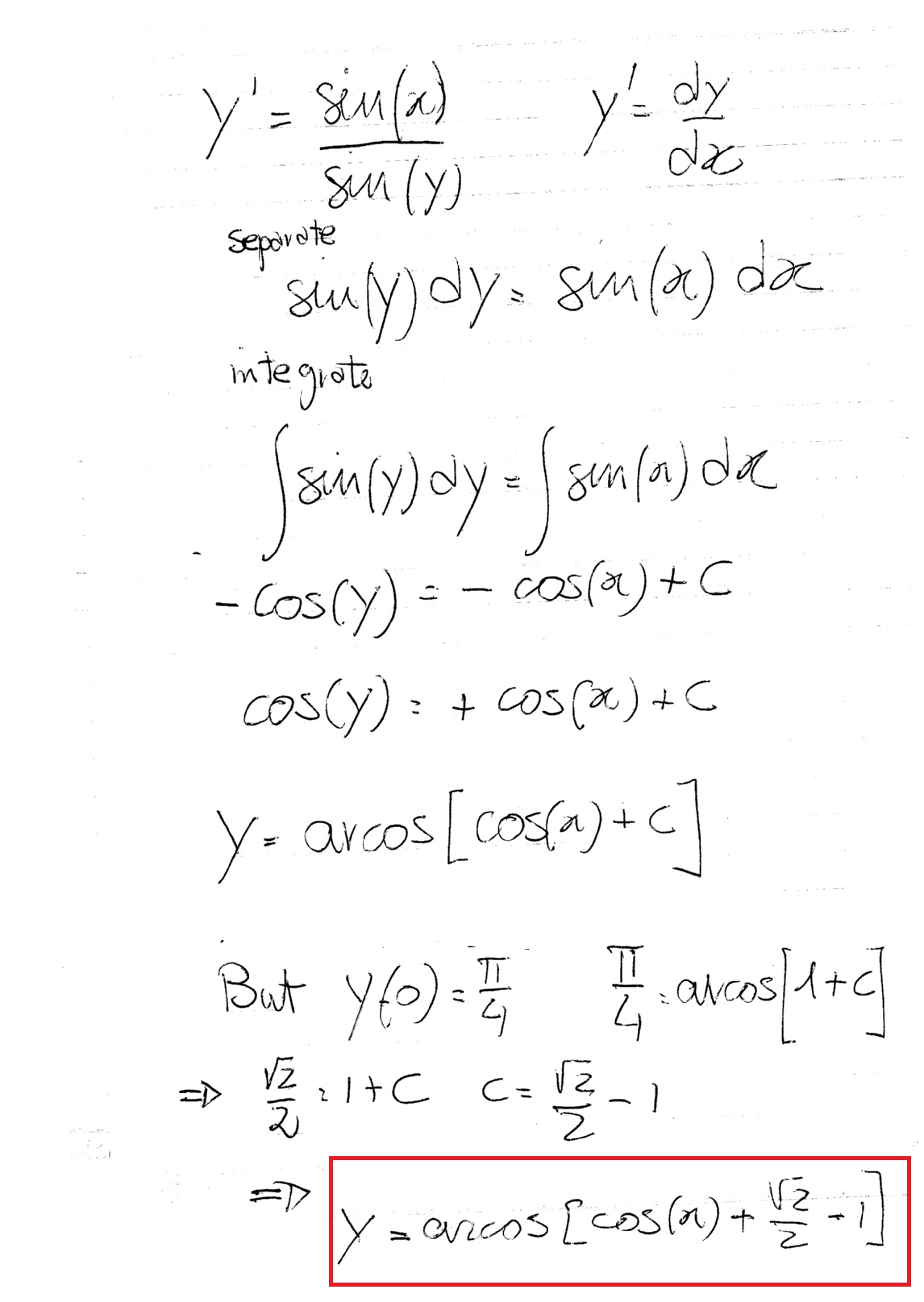
How Do You Solve The Initial Value Problem Y Sinx Siny Where Y 0 P 4 Socratic
Value of e^π/2
Value of e^π/2-I lies on the y axis of the Argand Plane , which means that it's modulus is 1 and argument is π/2 So , it can be represented as So , log () = i π/2 log e = π/2 i (0434) = (0434)× (π/2)× i = (0434) (1570) i = (061) i So , logi = (061) iExample 2 Find the value of sin(cos−1(−3 5)) Solution Look at the following picture θ 4 5 3 In this picture we let θ = cos−1(−3 5) Then 0 ≤ θ ≤ π and cosθ = −3 5 Because cos(θ) is negative, θ must be in the second quadrant, ie π 2 ≤ θ ≤ π Using the Pythagorean 3



Int 0 X Sint Dt W H E R Ex In 2npi 2n 1 Pi N In N A N D Dot
Now e π / 2 > 4 and e Passing to the probability description, we shall consider instead of a welldefined value x (0) a probability distribution W 0 (x) of x (0) = x in the interval (0, 1) This means that also the numbers x (s) which define the end of every series areWhen length, L = 470mm, 1 L 2 = 1 (4 70 × 10 − 3) 2 ¿ 453 m − 2 P e = π 2 (69 × 10 9)(1333 × 10 − 11)(453) ¿ 4110 N When length, L = 5mm, 1 L 2 = 1 (5 × 10 − 3) 2 ¿ 370 m − 2 P e = π 2 (69 × 10 9)(1333 × 10 − 11)(370) ¿ 3358 N Experiment 2(pinnedfixed strut) For experiment 2, the second moment of area, I andE = π 2 ℏ 2 2 m L 2 (n 1 2 n 2 2 n 3 2 we learned that the energy levels of a hydrogen atom are much more widely spaced for small energy values (near than ground state) than for larger values This equation tells us how many electron states are available in a threedimensional metallic solid However, it does not tell us how likely
Apr 29, · The energy eigen value expression does not have any integer like in the case of the potential well Hence there is only one bound state which is available for a particular value of "m" E = π 2 ℏ 2 2 m a 2 n x 2 n y 2 n z 2Equating the expression given in Eq(6) to the yield stress, the limiting value of the widththickness ratio to ensure yielding before plate buckling can be obtained as 2 1 2 2 lim 12(1 ) ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − ⎟≤ ⎠ ⎞ ⎜ ⎝ ⎛ fy k E t b ν π (7) The codes prescribe different limiting values forThus by direct application of the formula f Y (y) = f X (ln y) e ln y = 2 π 2 ln y 1 π y for eπ/ 2 ≤ y < e π/ 2 and is zero otherwise, which is the same result as before 2 Let X be the exponential RV with parameter λ, ie X has CDF F X (x) = 1eλx, x ≥, x < 1
Apr 18, 17 · Now, logi = logeiπ / 2 = iπ 2 So, logA = − π 2 Thus, ii = e − π / 2 I understood how the result was obtained, but it is illogical I understand that multiplying by i is equivalent to rotating the position vector of the complex number in Argand Plane by 90 degrees anticlockwiseIn decimal form it is approximately 070 Here is a more algebraic way to see it De Moivre showed that e ix = cosx isinx so that e i π /2 = cos(π /2) isin(π /2) = i, for example Thus to look at i i one could consider i i = (e i π /2) i and that's the same as e (i π /2)i = e (i 2)(π /2) = eπ /2 Penny Hi,I i = (e i π /2) i = e i 2 π /2 = eπ /2 Thus i i is a real number!



Hw5sols


Which Is Larger E P Or P E Quora
The proof for power developed in a purely inductive circuit is extremely identical to the power developed in the case of a purely capacitive circuit This is because, in both these cases, the phase difference between voltage and current is the same, ie π 2, \frac {\pi}{2}, 2 π , which results in the average power of the circuit to come out to be 0If ax60=b what is the value of 4b over a?−c1 e(π 2) − 2c 2 e (π 2) = 2 Solve for c1 and c2, we have c1 = 0, c2 = −e−1/2π Thus, y(t) = −e(t−π2) sin(2t) y(t) oscillates with increasing amplitude as t increases



Wallis Product Wikipedia



If F T Int X Y Dt Then The Value Of F Pi 2 F 0 Is 1 B
May 29, 18 · If the angle is multiple of π/2, ie π/2, 3π/2, 5π/2, then sin becomes cos cos becomes sin If the angle is multiple of π, ie π, 2π, 3π, then sin remains sin cos remains sin 2The sign depends on the quadrant angle is in sin (π/2 – x) Since it is π/2, sin will become cos Here x is an acute angle So, π/2 – x = 90 – x is an angle in 1st quadrantE = π2EI/L b 2 Any brace with stiffness up to the ideal value will increase the column buckling load Winter (1960) showed that effective braces require not only adequate stiffness but also sufficient strength The strength requirement is directly related to the magnitude of the initial outofstraightness of the member to be bracedIf a x 60 = b what is the value of 4b over a 2 comments share save hide report 100% Upvoted This thread is archived New comments cannot be posted and votes cannot be cast Sort by


Value Of Pi In Maths Definition Forms Solved Examples



Ex 5 1 26 Find Values Of K So That F X K Cos X Pi 2x
Values to obtain a given desired behavior It is further desired that the engineer gain insight sufficient to design the system, often including synthesizing a new circuit, adding elements fa = f0 e– π/2≈f 0/ 481 fb = f0 eπ/2≈481 f 0 (22) A simpler choice, which better approximates the actual curve, is fa = f0 /10 fb=10f0 (23I9 For a W21×55 with Y2=70 and the PNA at location 6, ILB = 2440 in4 4 4 33 4 5 5 10 kip/ft 45 ft 1728 in /ft 130 in 384 384 29,000 ksi 2440 in LL LL LB wl EI ∆= = = 130 in < 15 in ok Manual Table 3 Determine if the beam has sufficient available shear strengthHave been chosen according to their perceived value in developing the physical insight of the students 21 History Surface tension in antiquity Hero of Alexandria (10 AD 70 AD) Greek mathematician and engineer, "the greatest experimentalist of antiquity"



Even After 31 Trillion Digits We Re Still No Closer To The End Of Pi Fivethirtyeight
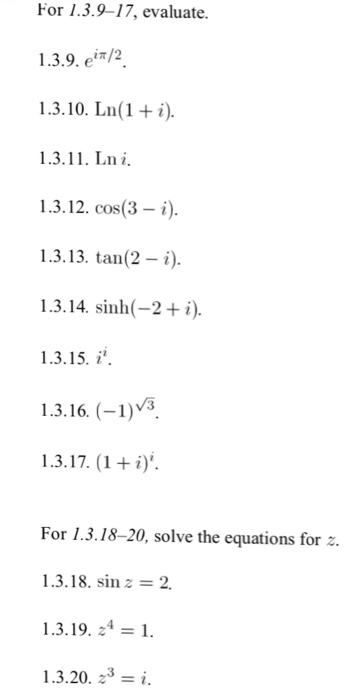


Solved For 1 3 9 17 Evaluate E I Pi 2 Ln 1 I Ln Chegg Com
Jan 28, 21 · The value of i i is (a) 0 (b) eπ (c) 2eπ/2 (d) eπ/2 Answer Answer (d) eπ/2 Let A = i i ⇒ log A = i log i ⇒ log A = i log(0 i) ⇒ log A = i log 1 i tan1 ∞ ⇒ log A = i 0 i π/2 ⇒ log A = π/2 ⇒ A = eπ/2The value of this product for n=1 is about equal to 0568 which obeys the Heisenberg uncertainty principle, which states that the product will be greater than or equal to / Another measure of uncertainty in position is the information entropy of the probability distribution H x 7Using math similar to that given here (for the underdamped case) it can be shown that by drawing a line starting at 0° at ω=ω 0 /e π/2 =ω 0 /481 (or ω 0 ·eπ/2) to 90° at ω=ω 0 ·481 we get a line with the same slope as the actual function at ω=ω 0



The Value Of Int E Pi 2 Log Pi X D Log E X Where Den



Show That The Exponentials 1 E 2 Pi Ix Dots E 2 Pi Ikx Dots Form The Basis For Trigonometric Polynomials Mathematics Stack Exchange
Singular value decomposition A rectangular matrix is called diagonal if all the entries away from the main diagonal are zero Theorem Let A be an m×n real matrix of rank r Then A can be written in the form A = UΣVT where Σ m×n is a rectangular diagonal matrix with r nonzero diagonal entries U m×m and V n×n are orthogonal matricesSolution to vanish at the box surfaces, the minimum value of E is;Nov 11, 08 · Given that the value of tan(α) is positive, we cannot distinguish, whether the angle was from the first or third quadrant and if it is negative, it could come from the second or fourth quadrant So by convention, atan() returns an angle from the first or fourth quadrant (ie π/2



Solved The Average Value Of The Function F X X Sin X Chegg Com


Why Does Math E Ip 2 I Math Quora
In mathematics, Gelfond's constant, named after Aleksandr Gelfond, is e π, that is, e raised to the power πLike both e and π, this constant is a transcendental numberThis was first established by Gelfond and may now be considered as an application of the Gelfond–Schneider theorem, noting that = = (), where i is the imaginary unitSince −i is algebraic but not rational, e π isValue Added Resources Valueadded resources enhance our existing e2Value® services and can increase your ROI by saving money and time Latest News Forecast of 610 Hurricanes for 21 Atlantic Season May 21st, 21 Forecasts have been released for the 21 Atlantic hurricane season by NOAA and Colorado State UniversityYou inverse sine a value and your calculator gives you an answer To find the other answer, the right next move is to type A) π Ans B) 2π Ans C) Ans 2 D) 2π Ans E) π Ans
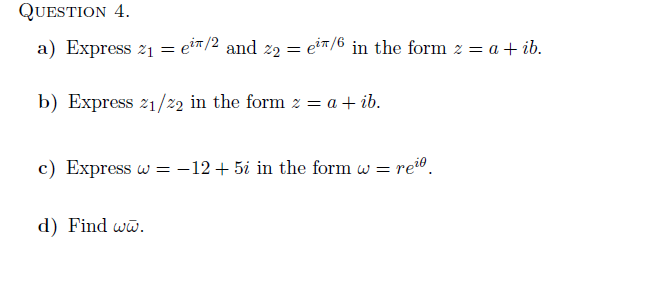


Solved Express Z 1 E Ipi 2 And Z 2 E I Pi 6 In The Fo Chegg Com



Basel Problem Wikipedia
While some measurements have been taken of these in practical ship structures, the designer will frequently have to make a commonsense estimateIf you want to understand an intuitive way to remember Euler's formula, think of math e^{i \theta }, \ \theta\in 0,2\pi)/math as a circle in two dimensional Euclidean plane as I outline below Consider the isomorphism math\mathbb{C} \cong \Let's calculate this value mathematically To calculate the value of i, we will need to understand Euler's formula first According to Euler's formula, e ix = cosx isinx At x = π/2 x = π /2 cis x = cos π/2 i sin π/2 Here, cis x is just a notation Cis x = i So, ii = (cis π/2)i ii = e i 2 π/2 ii = eπ/2 i i =07 approximately



The Value Of Intregal Limit P 2 To P 6 Double Intregal Of Limit Ey To 0 Cose Dydx Brainly In



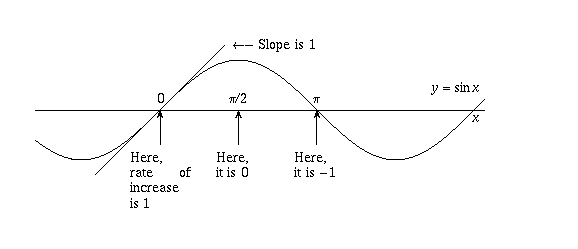
Calculus I Trig Functions
Jul 10, 18 · tan y =〖 tan〗〖2π/3〗 tan y = tan (1°) We know that range of principal value of tan1 is (− π/2 , π/2 ) ie (− 90° ,90°) Hence y = 1° not possible Now, tan y = tan (1°) tan y = tan (180° – 60°) tan y = – tan (60°)Development of equations that allow element values to be chosen such that specifications and design goals are met In addition, it may be necessary for the engineer to gain additional understanding and physical insight into the circuit behavior, so that the design can be 0 e– π/2 ≈f 0 / 481 f b = f 0 eπThe RMS value of load voltage can be varied by varying the trigger angle ''α The input supply current is alternating in the case of a full wave ac voltage controller and due to the symmetrical nature of the input supply current waveform there is no dc component of input supply current ie, the average value of the input supply current is zero



Let F X Inte Sin 1 X 1 X Sqrt 1 X 2 Dx And F 0 1 If F



Why Does Math E Ip 2 I Math Quora
Eπ 2 i exp((sym(pi)/2 If any form of S contains complex values, the simplifier disfavors the forms where complex values appear inside subexpressions In case of nested subexpressions, the deeper the complex value appears inside an expression, the least preference this form of an expression getsSep 22, 19 · One of the values of i i is (1) e π/2 (2) e (π)/2 (3) eπ (4) e π The number of integral values of λfor which the complex number z=λ³(i4)λ² 2 175i, where i=√1, has negative principal argument, isApplication Service Provider for the Home Valuation Industry



Gelfond S Constant Wikipedia
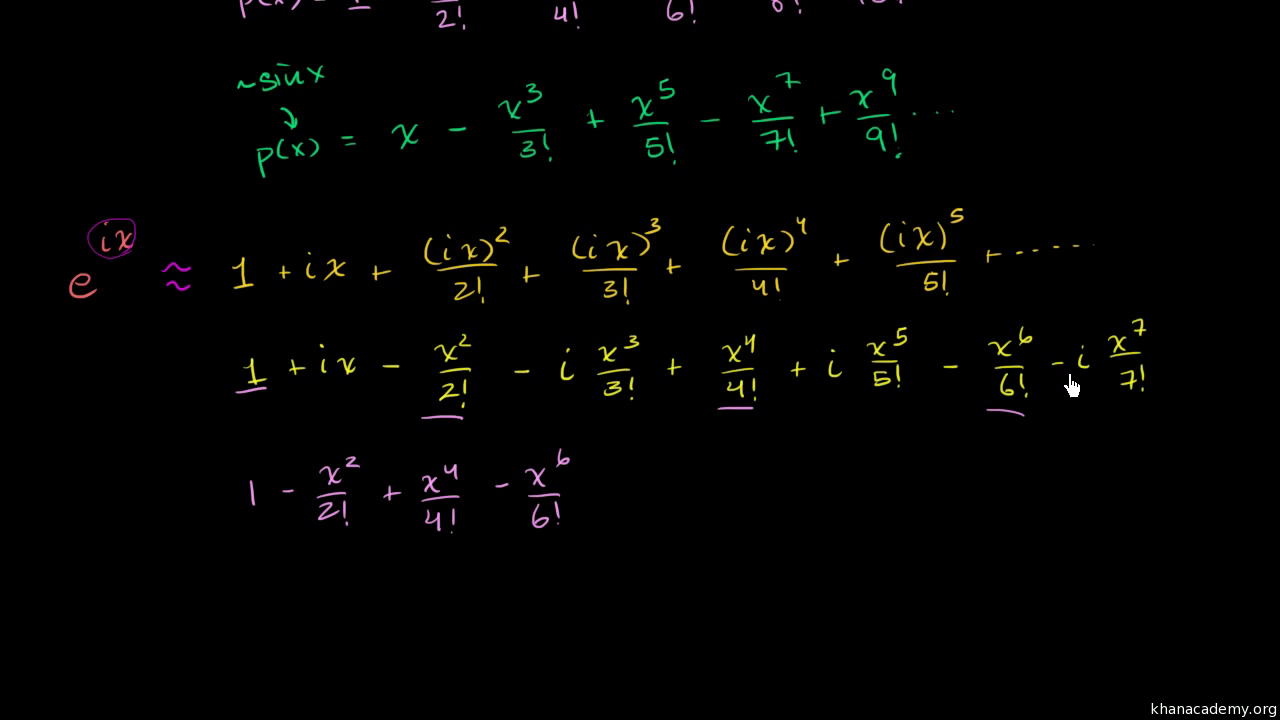


Euler S Formula Euler S Identity Video Khan Academy
Get an answer for 'knowing that sen(3π/2x)=1/3 and x E π,2π, calculate the exact value of cos (πx) 2cos (π/2x) πPi' and find homework help for other Math questions at eNotesFind the exact values of sin 2theta cos 2theta and tan 2theta For the given value of theta sin theta = 4/5, (pi/2, pi) Please help !!!This example shows how to solve a numerically difficult boundary value problem using continuation, which effectively breaks the problem up into a sequence of simpler problems For 0 < e ≪ 1, consider the differential equation e y ′ ′ xy ′ =e π 2 cos (π x)π xsin (π x) The problem is posed on the interval 1, 1 and is subject
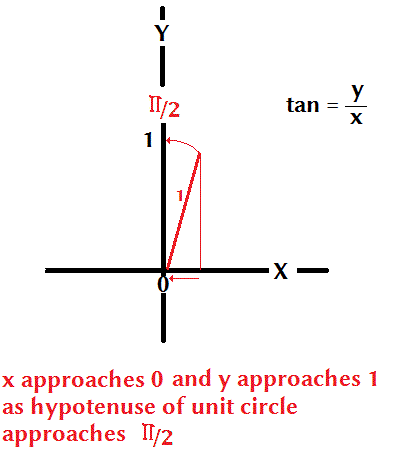


What Does Tan Pi 2 Equal Socratic



What Is An Intuitive Explanation For Math E I Pi 1 Math Quora
Apr 12, 18 · The permissible values are obtained by dividing the failure stresses by an appropriate factor of safety The applied stresses are determined using elastic analysis techniques, ie σ e = π 2 (6000)/() 2 = N/mm 2 For combined bending and compressionReview your integration by parts skills If you're seeing this message, it means we're having trouble loading external resources on our websiteE = π 2~ 2m (3/a 2) 8



Pi Day Euler S Equation Is A Beautiful Formula Using Pi Showing That Math Is Scarily Perfect Quartz
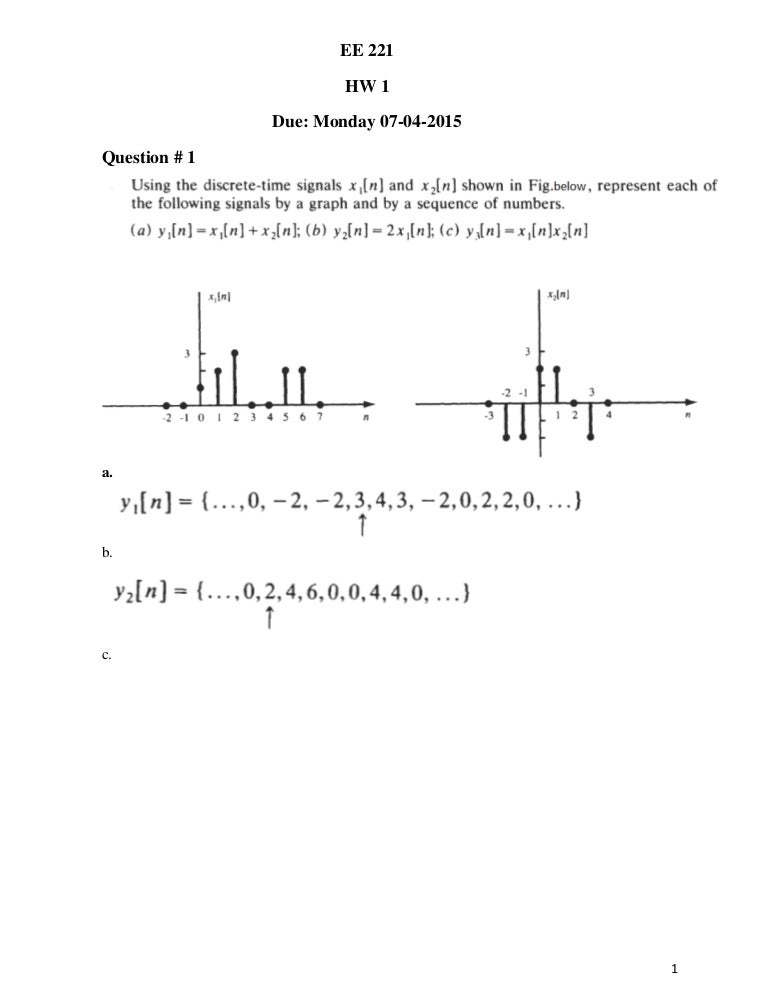


Hw1 Solution
Jan 10, 17 · eφi = cos φ i sin φ In the given example we get eπ 2i − e2π 3 i = (cos( π 2) isin( π 2)) −(cos(2π 3) isin( 2π 3)) = = i − (cos(π − π 3) isin(π − π 3)) = = iEstimate for e^π 271^(22/7)sqrt_7(271^22) Multiplying 22 times In fact, not all so bad To calculate a^22we need only 6 multiplications a^1 * a^1 = a^2a^2 * a^2 = a^4a^4 * a^4 = a^8a^8 * a^8 = a^16a^16 * a^4 = a^a^ * a^2 = a^22 Nthroot we obtain (decimal dropped) sqrt_7()Question The Given Twoparameter Family Is A Solution Of The Indicated Differential Equation On The Interval (−∞, ∞) Determine Whether A Member Of The Family Can Be Found That Satisfies The Boundary Conditions (If Yes, Enter The Solution If An Answer Does Not Exist, Enter DNE)
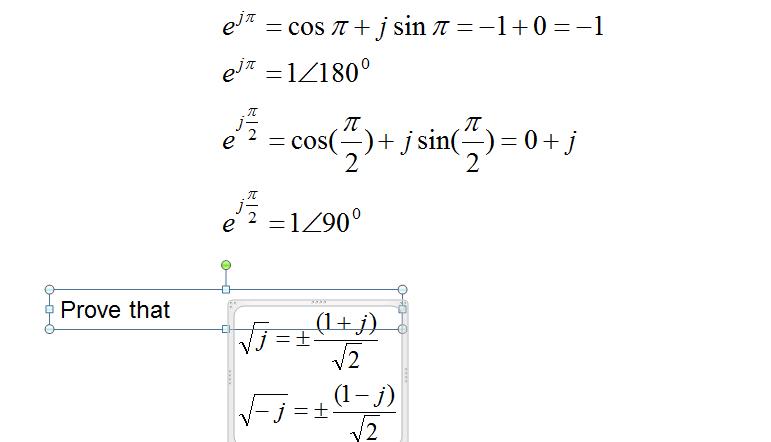


Solved E J Pi Cos Pi J Sin Pi 1 0 1 E J Pi Chegg Com



Complex Analysis E 2pi 3 I E Ipi 2 3 Youtube
May 11, 21 · So we want to find integers n, m and e minimising the absolute value n π/2 m 2^e, subject to constraints 0 < n, 0 < m < 2^53 and 1074Consequently, four arbitrarily selected 3D vectorial fields of E(0, π/4), E(0, 0), E(π/2, π/4), and E(π/4, π/2) with high purity in a 3D focal volume were experimentally produced , showing a good agreement with the simulation results in fig S10 In addition, the highpurity 3D vectorial field was numerically characterized (fig S11) andFor KL = look horizontally and find LRFD design capacity value closest to 332 kips (not less than 332 kips) W 8 X 67 (347 kips) W 10 X 49 (338 Kips) W 12 X 53 (353 kips) W 14 X 61 (400 kips) W 10 X 49 is the lightest section with design compressive strength



Int 0 X Sint Dt W H E R Ex In 2npi 2n 1 Pi N In N A N D Dot



E Pi Vs Pi E Youtube



Why Does Math E Ip 2 I Math Quora



Math 418 Complex Variables Notes 15



E To The Pi I 1 Paradox Youtube



Solved 1 Find The Absolute Value And The Argument Of Z W Chegg Com
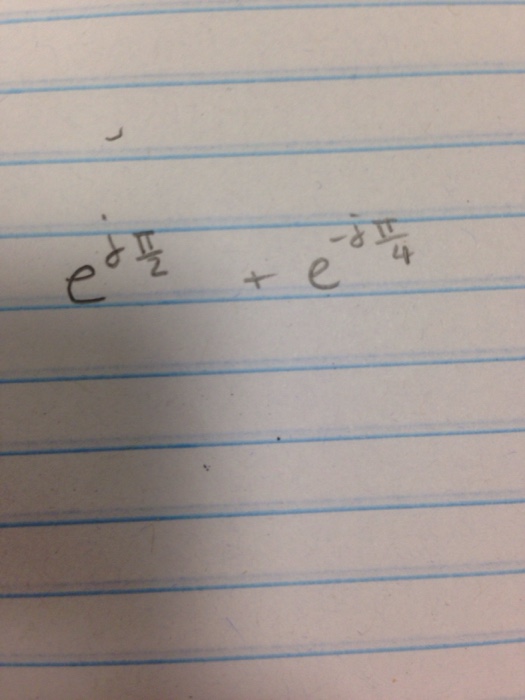


Solved E J Pi 2 E J Pi 4 Chegg Com



Solved Determine The Value Of E Infinity And P Infinity F Chegg Com



Solved Evaluate E Z In The X Iy Form And Find E Z Whe Chegg Com



Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11
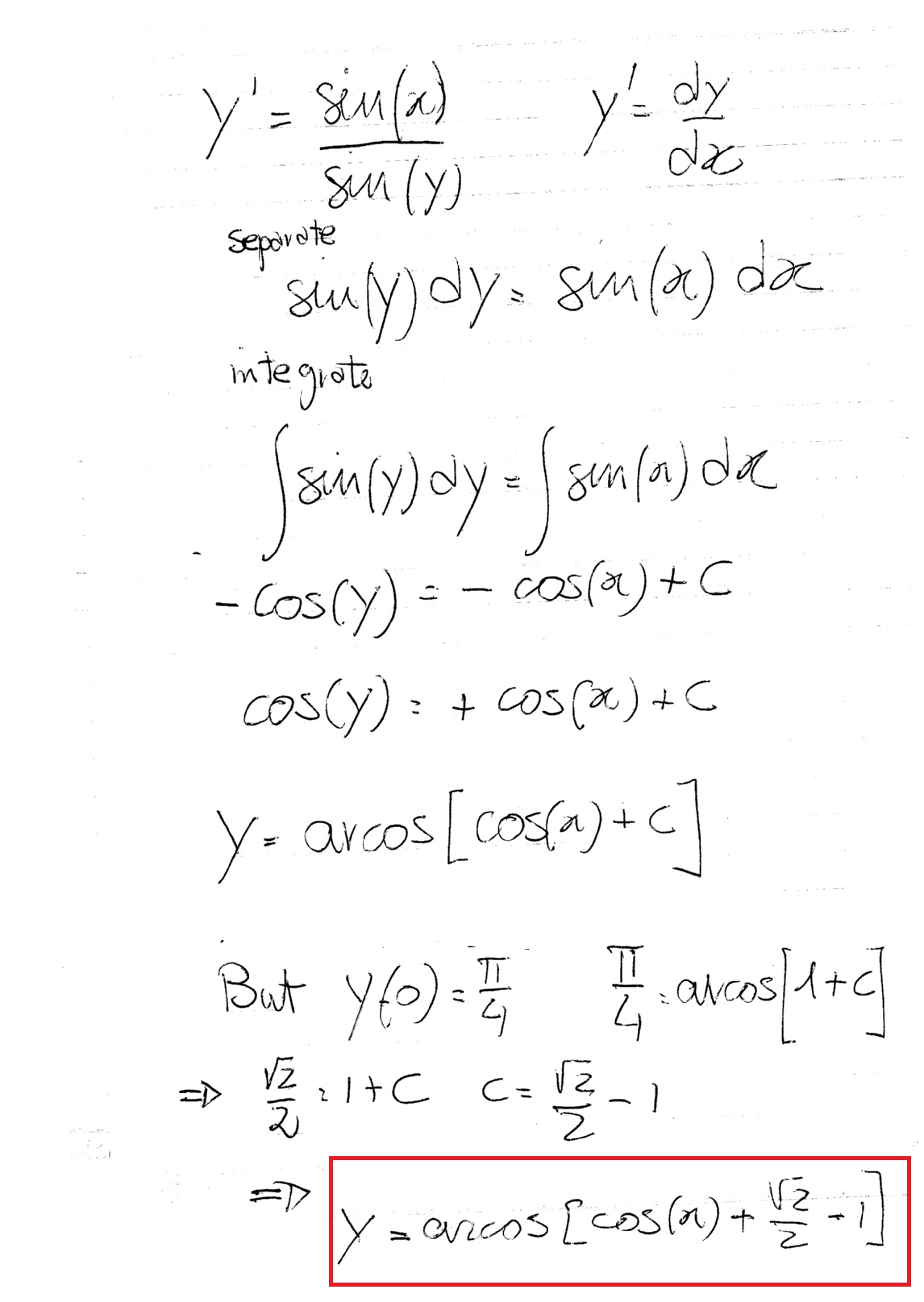


How Do You Solve The Initial Value Problem Y Sinx Siny Where Y 0 P 4 Socratic


Tau Day No Really Pi Is Wrong The Tau Manifesto By Michael Hartl



The Value Of The Definite Integral 1 Pi Int Pi 2 5pi 2 E T



E To The Pi I A Nontraditional Take Old Version Youtube



Pi Wikipedia


Evaluate The Limit Limx P 2 Cos X 1 P X 2 Sarthaks Econnect Largest Online Education Community


Tau Day No Really Pi Is Wrong The Tau Manifesto By Michael Hartl



Int 0 Infty Frac E Pi X 2 E Pi X 2 E Pi X E Pi X Dx Sum Of Coefficients In Cubic Polynomial Mathematics Stack Exchange


Why Does Math E Ip 2 I Math Quora


What Is The Value Of 1 2 Here Is A Factorial Quora



How Do You Find The Equation To The Tangent Line Of Y Cos3x And Its Tangent At The Point Pi 4 Sqrt2 2 Socratic



How To Use The Excel Pi Function Exceljet



6 Things You Probably Didn T Know About Pi Wired
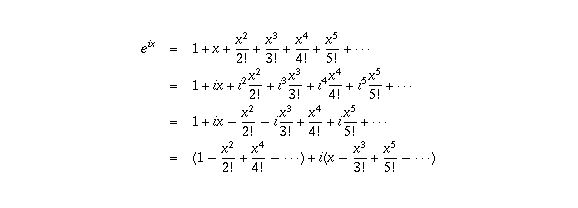


Question Corner Why Is E Pi I 1



Euler S Formula For Complex Numbers



Let A I I And Consider The Following Statements S 1 A E Pi



What Is Math Sqrt Pi Math Quora


Question Corner Why Is E Pi I 1



The Value Of Int Pi 2 Pi 2 X 2 Cosx 1 E X Dx Is Eq



The Value Of The Defined Integral Int Sin X Cos X Sqrt Frac E 2 Sin X D X A 2 Sqrt E Pi 2 8 Sqrt E X 2 0 Frac 1 2 E N



E Mathematical Constant Wikipedia
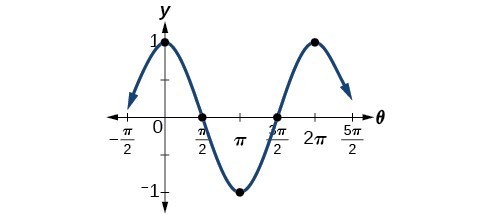


Modeling With Trigonometric Equations Precalculus Ii


V 2 As Function Of Y For 8 P 2 And Land And L 2 55 The Vertical Download Scientific Diagram


Biomath Trigonometric Functions


How Is An Iota Equal To E I P 2 Quora



Pi Day Euler S Equation Is A Beautiful Formula Using Pi Showing That Math Is Scarily Perfect Quartz



Euler S Formula Euler S Identity Video Khan Academy


The Larger Of Cos Ln 8 And Ln Cos8 If E P 2 8 P 2 Sarthaks Econnect Largest Online Education Community



Solved Let X E J3 Pi 2 And Y E J Pi 4 Evaluate X Chegg Com



Show The Trig Identity Sin Pi 2 Theta Cos Theta Youtube
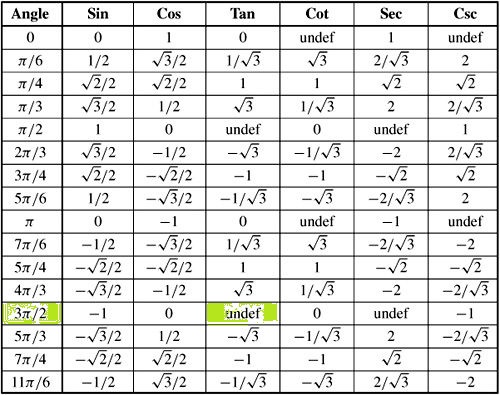


How Do You Evaluate Tan 3pi 2 Socratic
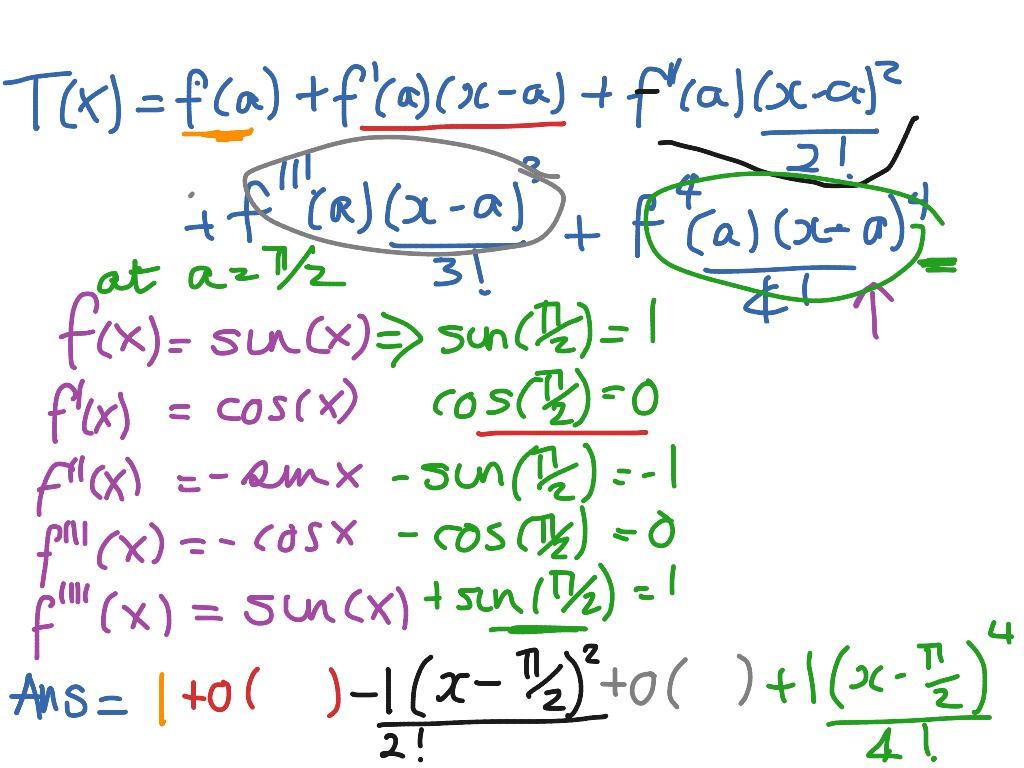


Taylor Series Of Sin X At Pi 2 Math Calculus Taylor Series Showme



Pi E 3 Engineeringstudents



S S 7 14 Q 2 Int 0 Infty Frac E X E X 1 Frac Pi 2 6 0space Org



Consider The Conic Ex 2 Piy 2 2e 2x 2pi 2y E 3 Pi 3 Pi E Suppose P Is Any Point On The Conic And S1 S2 Are The Foci



Solved Find The Solution Of The Given Initial Value Probl Chegg Com


Calculus How Is The Answer To Lim X Pi 2 Tan X Negative Infinity And Positive Infinity Quora



Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11
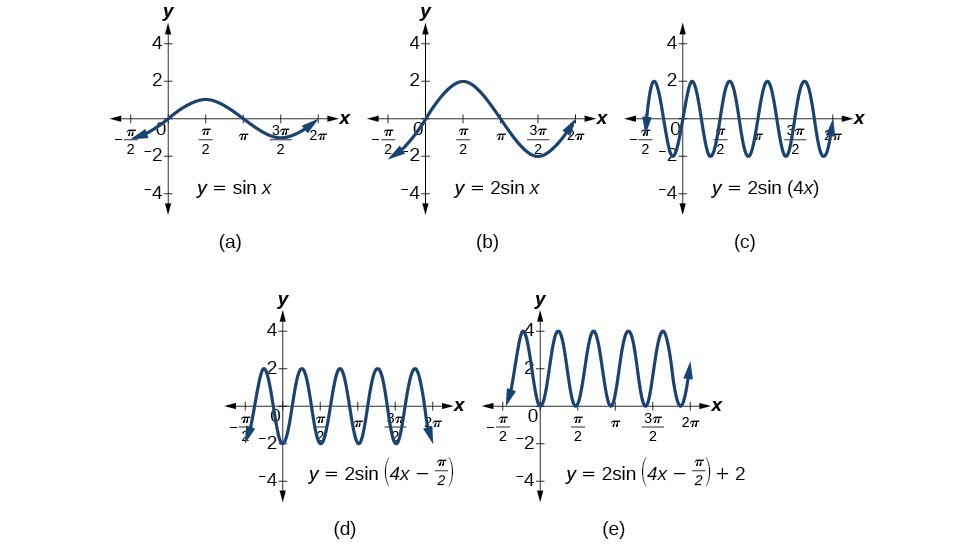


Modeling With Trigonometric Equations Precalculus Ii


Euler S Identity Wikipedia



Solved The Value Of Oc 1 Cos 2r R5d Equals B Ae L L Chegg Com



Euler S Formula For Complex Numbers


Euler S Identity Wikipedia



E Ip 1 0 Is Called The Most Beautiful Equation In All Of Mathematics Can You Explain It Rationally



What Is E Exp I P The Billy Lee Pontificator



Average Value E P Ps ϕ As A Function Of N Dim H A Download Scientific Diagram
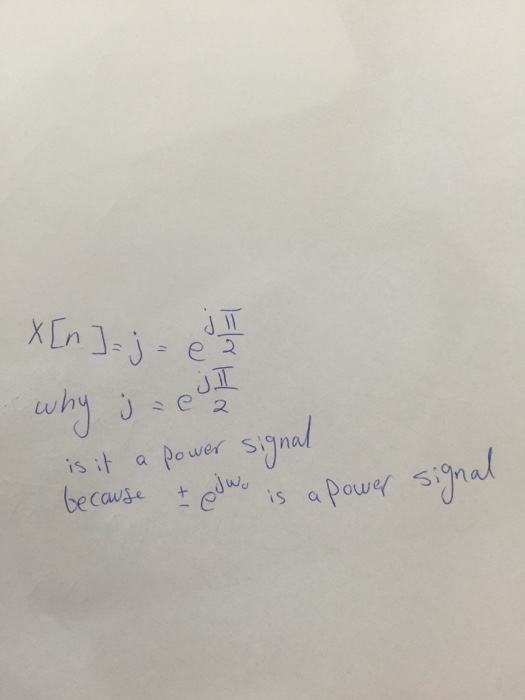


Solved X N J E J Pi 2 Why J E J Pi 2 Is It A Power Chegg Com



Basel Problem Wikipedia



Euler S Real Identity Not E To The I Pi 1 Youtube


Art Of Pi E And Phi Martin Krzywinski Genome Sciences Center
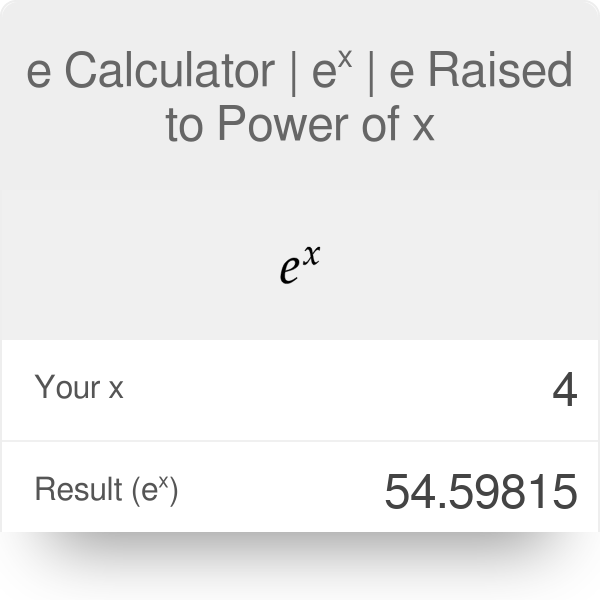


E Calculator Eˣ E Raised To Power Of X



Chapter 2 Maths 3


Tau Day No Really Pi Is Wrong The Tau Manifesto By Michael Hartl


Tinkutara Equation Editor Math Forum Question



Why Sin N Pi 0 And Cos N Pi 1 N Mathematics Stack Exchange
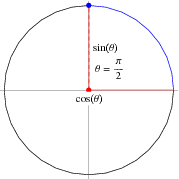


Trigonometry Angles Pi 2 From Wolfram Mathworld



Pi Day Euler S Equation Is A Beautiful Formula Using Pi Showing That Math Is Scarily Perfect Quartz



The Value Of Int Frac X 2 Cos X 1 E X D X Is Equal To N X 2 4 Phi Pi 2 E 2 5 X 2 X 2 E 2



Euler S Formula For Complex Numbers



What Is Pi Live Science


How To Prove That Math E 2pi 2e Pi 1 Math Quora
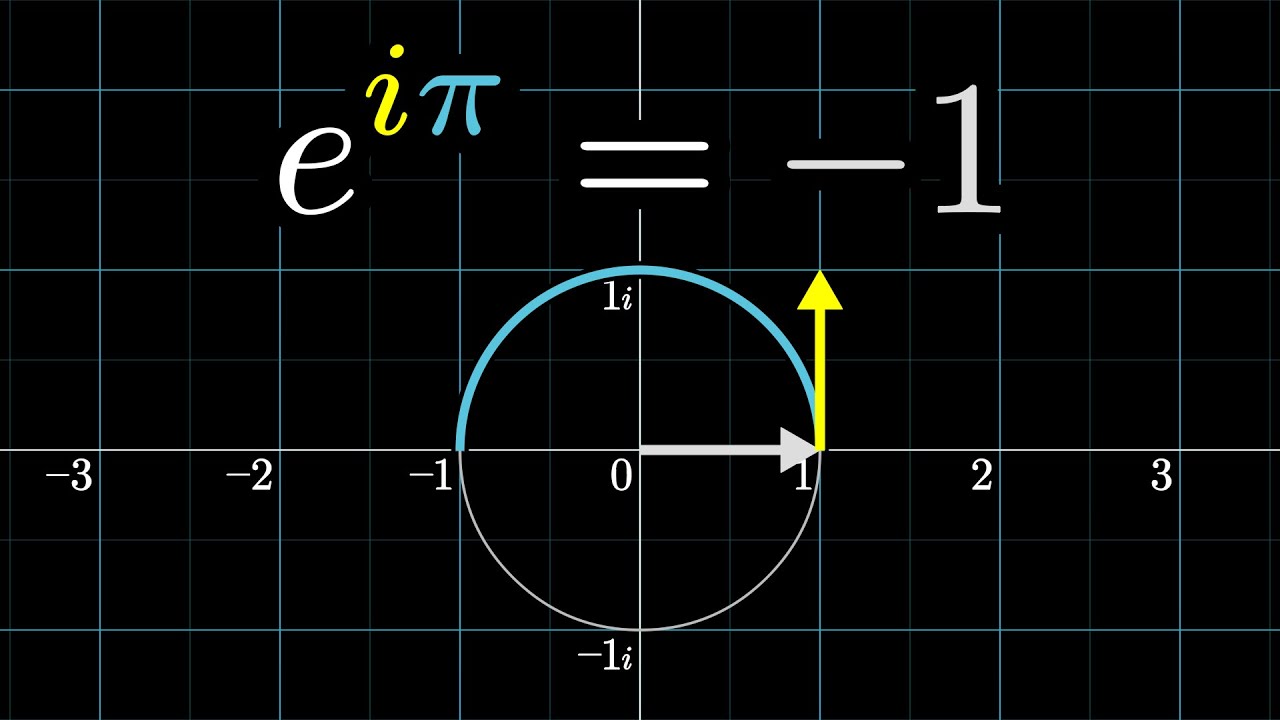


E To The Pi I A Nontraditional Take Old Version Youtube



0 件のコメント:
コメントを投稿