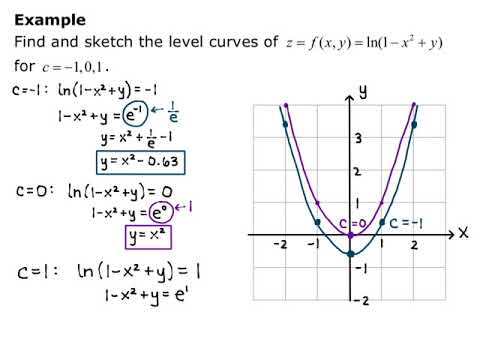
Section 15 Functions of Several Variables In this section we want to go over some of the basic ideas about functions of more than one variable First, remember that graphs of functions of two variables, z = f (x,y) z = f ( x, y) are surfaces in three dimensional space For example, here is the graph of z =2x2 2y2 −4 z = 2 x 2 2 y 2 − 4Level surfaces Scroll down to the bottom to view the interactive graph Level surface are basically the same as level curves in principle, except that the domain of \(f(x,y,z)\) is in 3Dspace Therefore, the set \(f(x,y,z) = k\) describes a surface in 3Dspace rather than a curve in 2DspaceSketch some level curves of the function Solution First, let z be equal to k, to get f(x,y) = k Secondly, we get the level curves, or Notice that for k>0 describes a family of ellipses with semiaxes and Finally, by variating the values of k, we get graph bellow (Figure 3), called, level curves or contour map Firgure 3 Level curves of

16 1 Functions Of Several Variables
Level curve grapher 3d
Level curve grapher 3d-Level curves Graph several level curves of the following functions using the given window Label at least two level curves with their zvalues z=x^{2}y^{2} ;Level curves The two main ways to visualize functions of two variables is via graphs and level curves Both were introduced in an earlier learning module Level curves for a function z = f ( x, y) D ⊆ R 2 → R the level curve of value c is the curve C in D ⊆ R 2 on which f C = c Notice the critical difference between a level curve C




Level Sets Math Insight
Online 3D Function Grapher A standalone application version of this 3D Function Graphing Program, written in Flash Actionscript, much faster, essentially more capabilities, builtin function calculator and many more This tool graphs z = f (x,y) mathematical functions in 3DThese level curves express a function value that is always constant through the curve f(x,y) = k f ( x, y) = k , and the gradient of the curve has a perpendicular direction to the graph When weLevel Curve Grapher Level Curve Grapher Enter a function f (x,y) Enter a value of c Enter a value of c Enter a value of c Enter a value of c
Definition The level curves of a function f of two variables are the curves with equations f (x,y) = k, where k is a constant (in the range of f) A level curve f (x,y) = k is the set of all points in the domain of f at which f takes on a given value k In other words, it shows where the graph of f has height k Graphing Calculator is a tool for quickly visualizing math You type an equation and Graphing Calculator draws it for you without complicated dialogs or commands Graph functions in two, three, and four dimensions, explicit, implicit, or parametric Graph inequalities, contour plots, density plots and vector fields 1624 // Summary for how to sketch level curves Whenever you're dealing with a multivariable function, the graph of that function will be a threedimensional figure in space If you take a perfectly horizontal sheet or plane that's parallel to the xyplane, and you use that to slice through your threedimensional figure, then what you get at
Question Level curves Graph several level curves of the following functions using the given window Label at least two level curves with their zvalues z = 2x y;New url for the 3D plotter https//wwwmonroeccedu/faculty/paulseeburger/calcnsf/CalcPlot3D/This video explains how to graph contour plots for functions o Level Curve A level set in two dimensions Phase curves are sometimes also known as level curves (Tabor 19, p 14) SEE ALSO Contour Plot, Equipotential Curve, Level Surface, Phase Curve REFERENCES Tabor, M Chaos and Integrability in Nonlinear Dynamics An Introduction New York Wiley, 19



Http Web Math Ucsb Edu Rackermann 5bgraphinganddirderivs Pdf



Level Set Wikipedia
Level Curves Def If f is a function of two variables with domain D, then the graph of f is {(x,y,z) ∈ R3 z = f(x,y) } for (x,y) ∈ D Def The level curves of a function f(x,y)are the curves in the plane with equations f(x,y)= kwhere is a constant in the range of f The contour curves are the corresponding curves on the surface, theGet certified as an expert in up to 15 unique STEM subjects this summerRelief Functions and Level Curves Purpose The purpose of this lab is to introduce you to plots of relief functions and level curves on surfaces Several Maple procedures will be introduced to help with visualization Background then use plot3d to see this 3dimensional graph
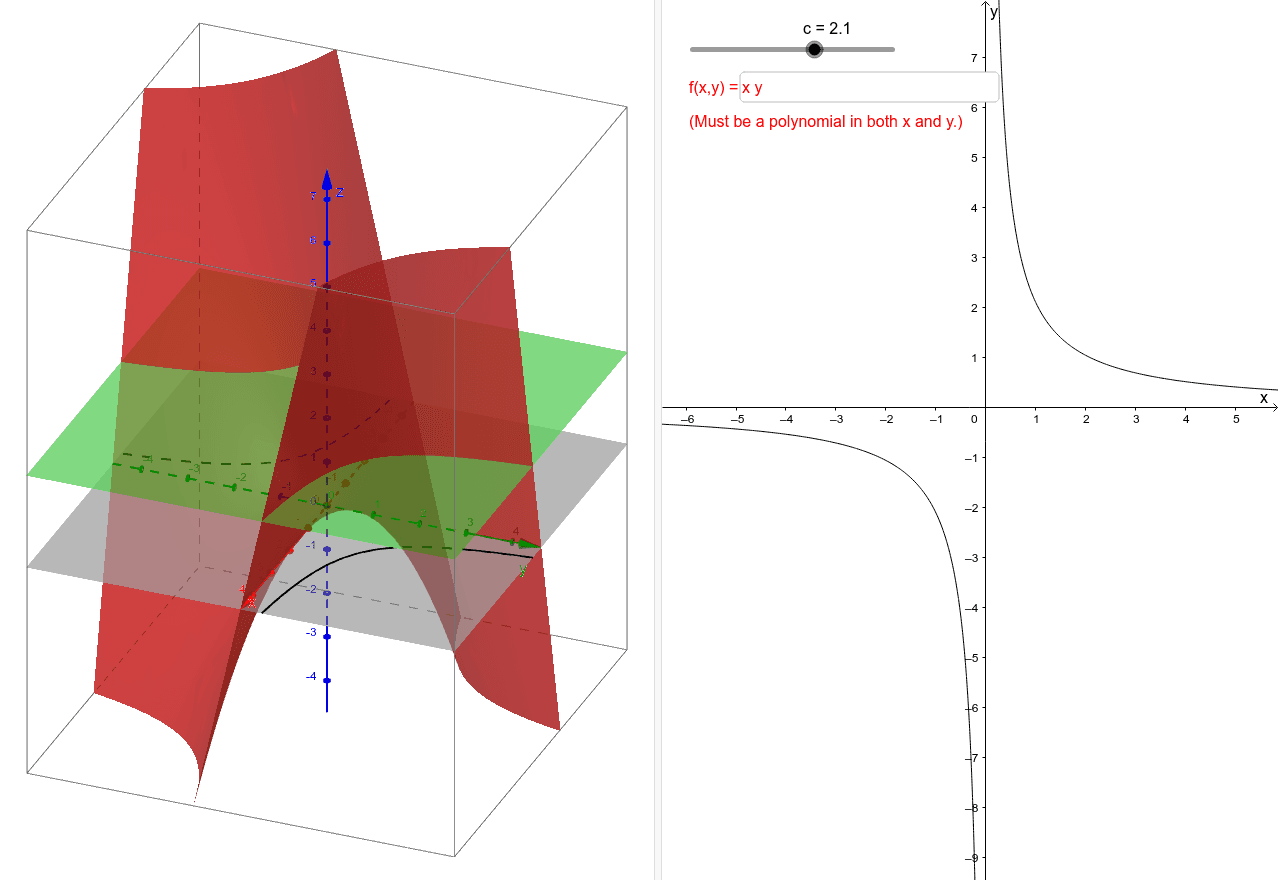



Level Curves Geogebra



1
One way to collapse the graph of a scalarvalued function of two variables into a twodimensional plot is through level curves A level curve of a function f (x, y) is the curve of points (x, y) where f (x, y) is some constant value A level curve is simply a cross section of the graph of z = f (x, y) taken at a constant value, say z = cWe will study the level curves c = x 2 − y 2 First, look at the case c = 0 The level curve equation x 2 − y 2 = 0 factors to (x − y) (x y) = 0 This equation is satisfied if either y = x or y = − xLevel Curves One way to visualize what a function's graph might look like is to create a topographic projection of the function inside its domain region These topographic projections are called level curves or contour curves for the function zfxy= (,) Ex) Sketch the level curves for the function f(,)xy y x= 2 − using z = 0, 1, 2 and 3
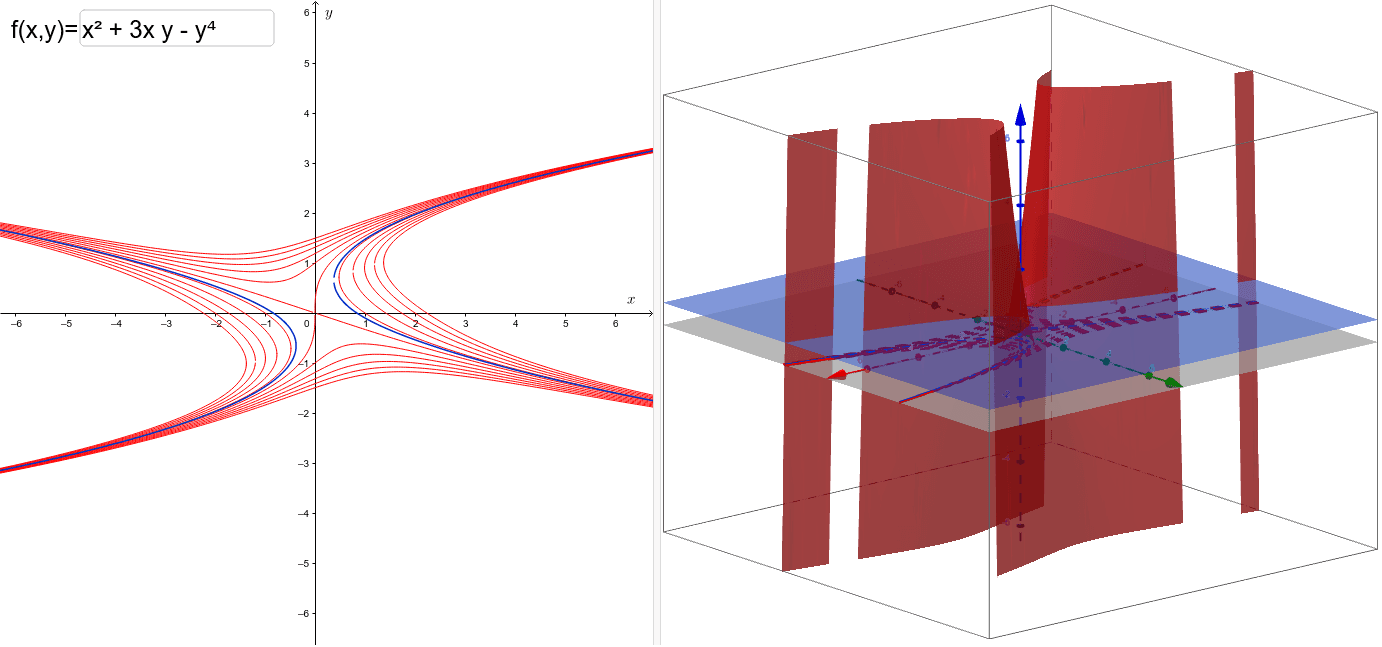



Level Curves Geogebra
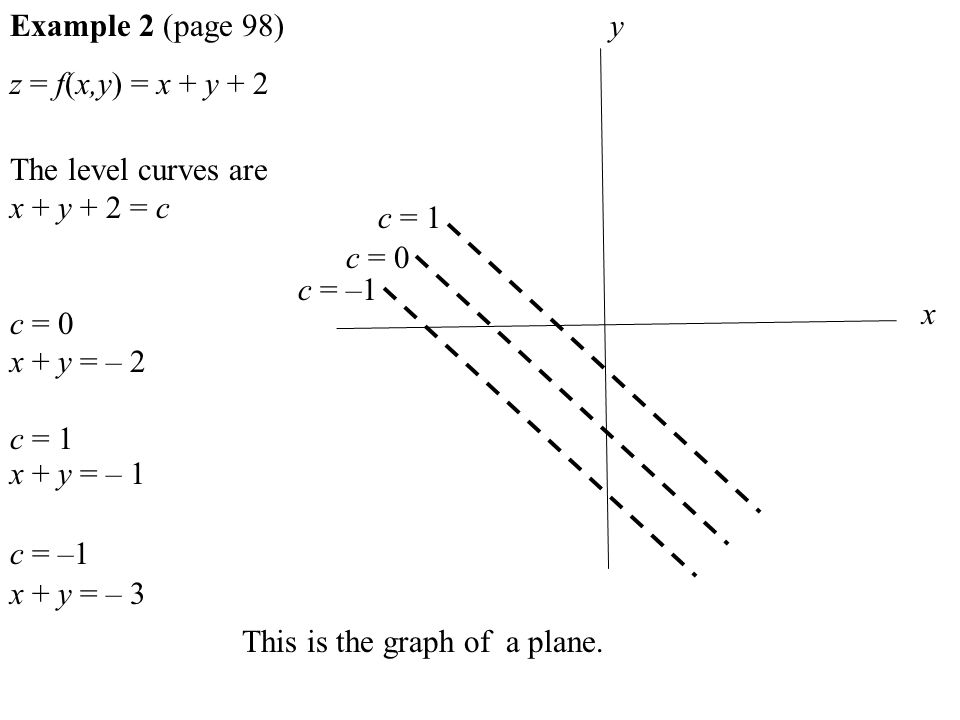



If X X1 X2 Represents A Point In A Subset A Of Rn And F X Is Exactly One Point In Rm Then We Say That F
Y (a) (b) Figure 1314 Graphing the level curves in Example 1313 The level curves are shown in Figure 1314 (a) Note how the level curves for c = 0 and c = 02 are very, very close together this indicates that f is growing rapidly along those curvesLevel curves Scroll down to the bottom to view the interactive graph A level curve of f (x, y) is a curve on the domain that satisfies f (x, y) = k It can be viewed as the intersection of the surface z = f (x, y) and the horizontal plane z = k projected onto the domainLevel Curves and Contour Plots Level curves and contour plots are another way of visualizing functions of two variables If you have seen a topographic map then you have seen a contour plot Example To illustrate this we first draw the graph of z = x2 y2 On this graph we draw contours, which are curves at a fixed height z = constant




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware



Level Curves Are Shown For A Function F Determine Whether The Following Partial Derivatives Are Positive Or Negative At The Point P A F X B F Y C F
Free ebook http//tinyurlcom/EngMathYT How to sketch level curves and their relationship with surfaces Such ideas are seen in university mathematics andFree graphing calculator instantly graphs your math problemsLevel curves Loading level curves level curves Log Inor $$ ≤ $$ ≥ $$ 1 $$ 2 $$ 3 $$ − A B C $$ $$ π $$ 0 $$ $$ = $$ Sign UporLog In to save your graphs!
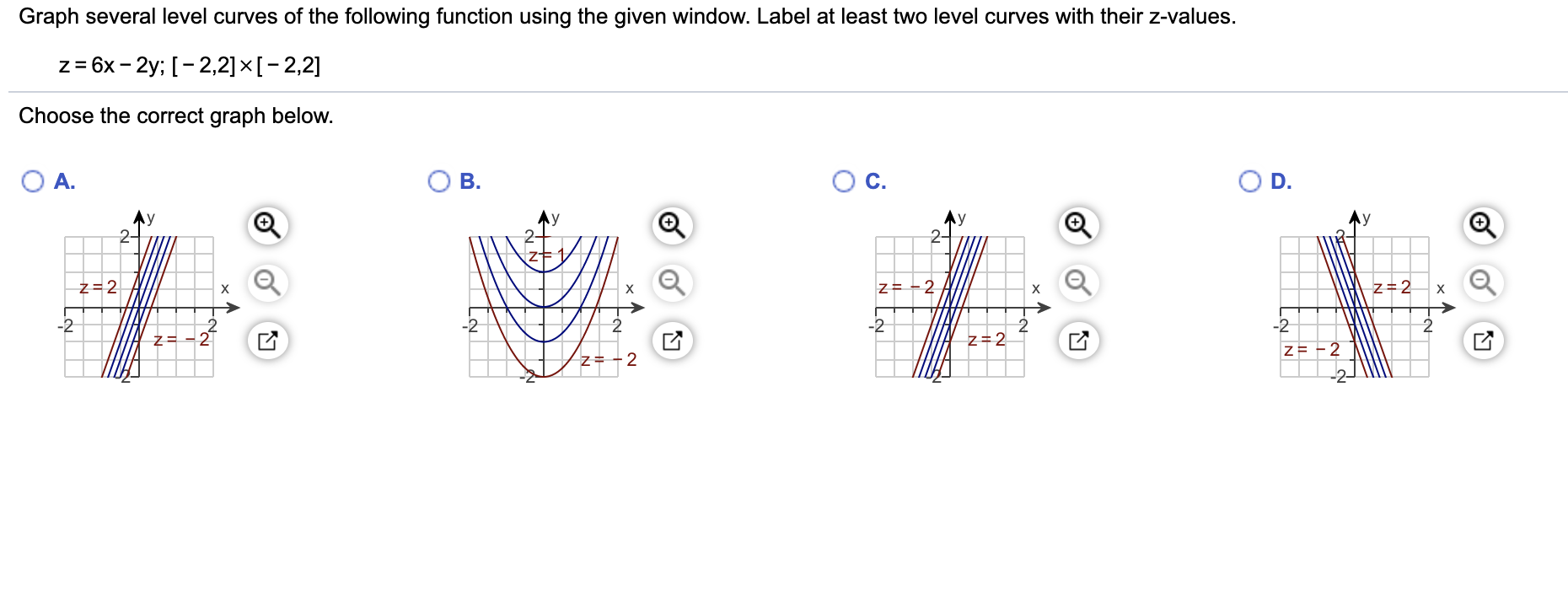



Graph Several Level Curves Of The Following Function Chegg Com




Level Curves Geogebra Dynamic Worksheet
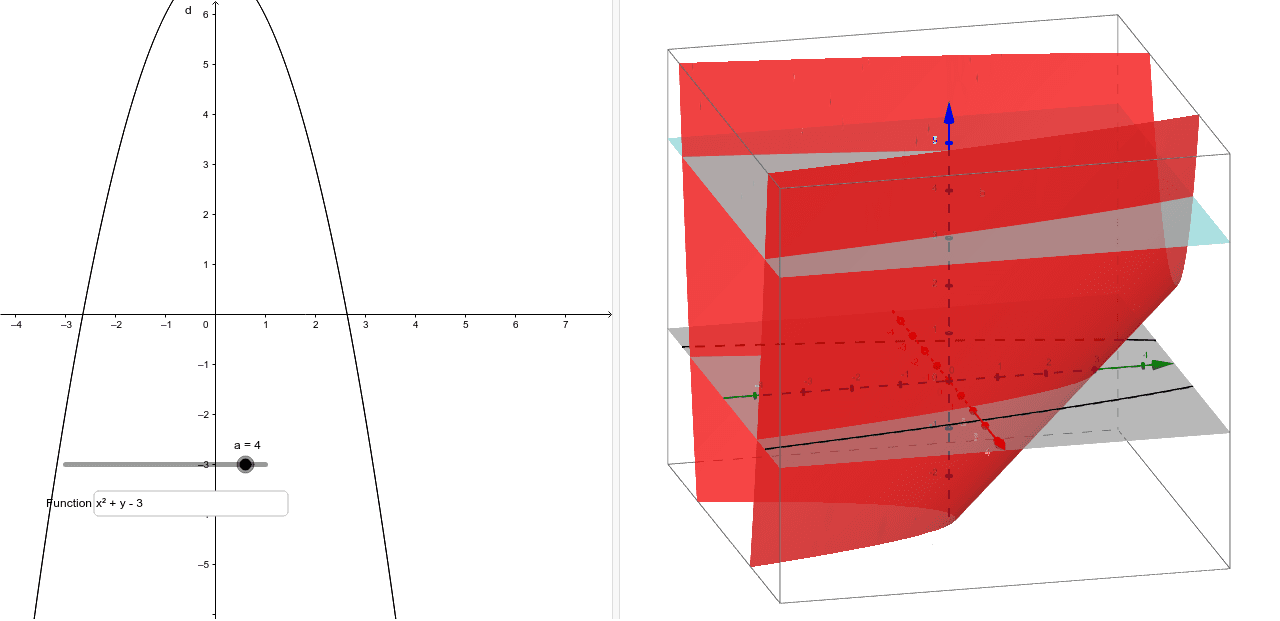
Level surfaces For a function $w=f(x,\,y,\,z) \, U \,\subseteq\, {\mathbb R}^3 \to {\mathbb R}$ the level surface of value $c$ is the surface $S$ in $U \subseteqIe the level curves of a function are simply the traces of that function in various planes z = a, projected onto the xy plane The example shown below is the surface Examine the level curves of the function Sliding the slider will vary a from a = 1 to a = 1 IS curve is a schedule/curve that shows the equilibrium output level that occurs in the market for goods and services at different levels of interest The IS curve is one part of the ISLM model and it is plotted with interest on yaxis and output on xaxis The equilibrium in the goods market depends on the interplay of aggregate demand (expenditure) and income



Level Sets Ximera




Level Curves And Cross Sections Maple Help
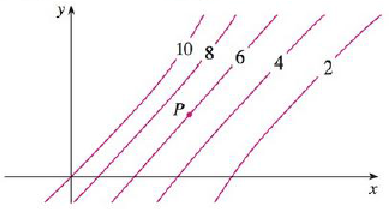
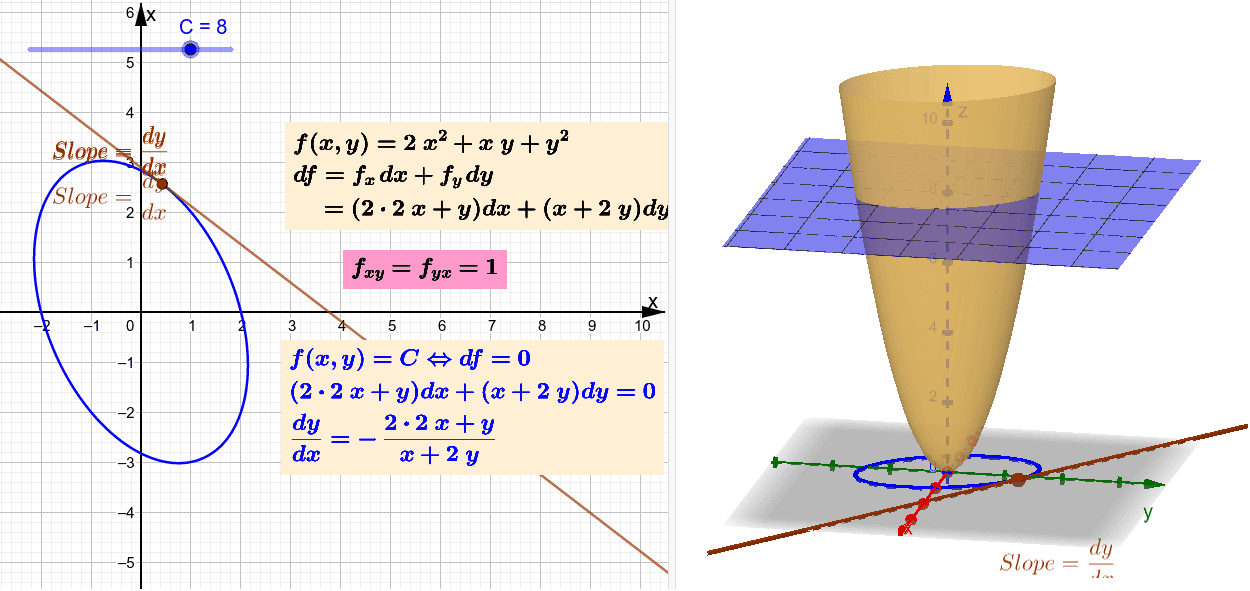
New Blank Graph Examples Lines Slope Intercept Form example Lines Point Slope Form example Lines Two Point Form Family of sin Curves example Lists CurveThere is a close relationship between level curves (also called contour curves or isolines) and the gradient vectors of a curve Indeed, the two are everywhere perpendicular This handout is going to explore the relationship between isolines and gradients to help us understand the shape of functions in three dimensions This is a common application in physics when considering lines ofLEVEL CURVES The level curves (or contour lines) of a surface are paths along which the values of z = f(x,y) are constant;
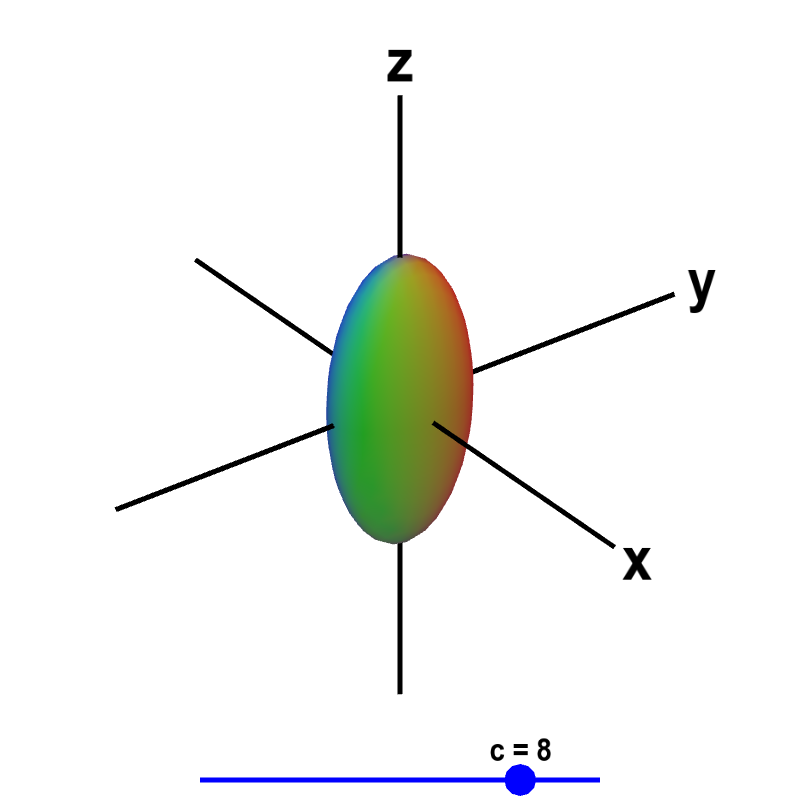



Level Sets Math Insight
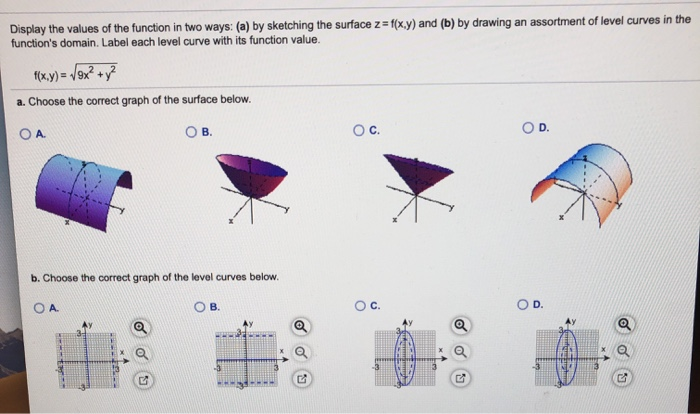



Display The Values Of The Function In Two Ways A Chegg Com
The directional derivative of a function is the rate of change of that function if the argument is changed in a particular direction Because a function has constant value along a level curve, the directional derivative is zero in the direction tangent to the level curve We draw the level curve with the tangent vector atIn the demo above, every point in the graph has an x and y value Each point also has a z value which is calculated by plugging the x and y values in to the expression shown in the box By default this expression is x^2 y^2 So if x = 2, and y = 2, z will equal 4Get the free "Plotting a single level curve" widget for your website, blog, Wordpress, Blogger, or iGoogle Find more Mathematics widgets in WolframAlpha



12 1 Introduction To Multivariable Functions Mathematics Libretexts
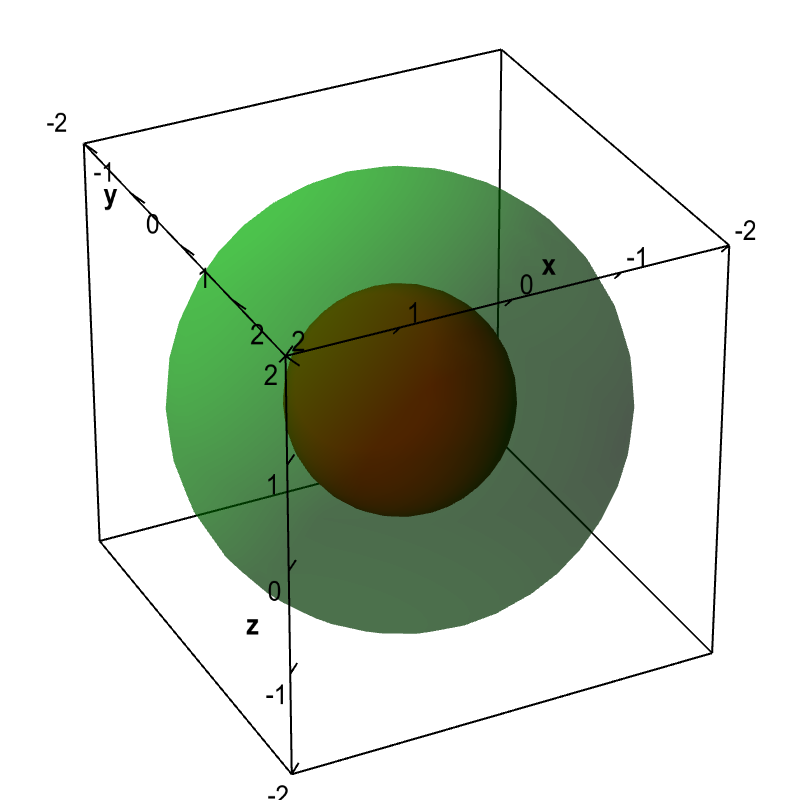



Level Set Examples Math Insight
Looking for the level curve xy = 3 to the graph xy= z graphingfunctions Share Cite Follow edited Sep 17 ' at 1450 Sedumjoy asked Jul 18 '17 at 2307 Sedumjoy Sedumjoy 1,371 10 10 silver badges 25 25 bronze badges $\endgroup$ 7What this means is that we are only good at drawing level curves of the following types The graph of a function y = g (x) A "sideways" graph of the form x = g (y) A conic section such as a circle, ellipse, or hyperbolaAdd to graph Function z=f(x,y) Space Curve r(t) Vector Field Point (x, y, z) Vector Text Label Implicit Surface Parametric Surface Region Slider ────────── Function r=f(θ,z) Function z=f(r,θ) Function ρ=f(θ,φ) Function x=f(y,z) Function y=f(x,z) Surface of Revolution




Level Sets Ximera
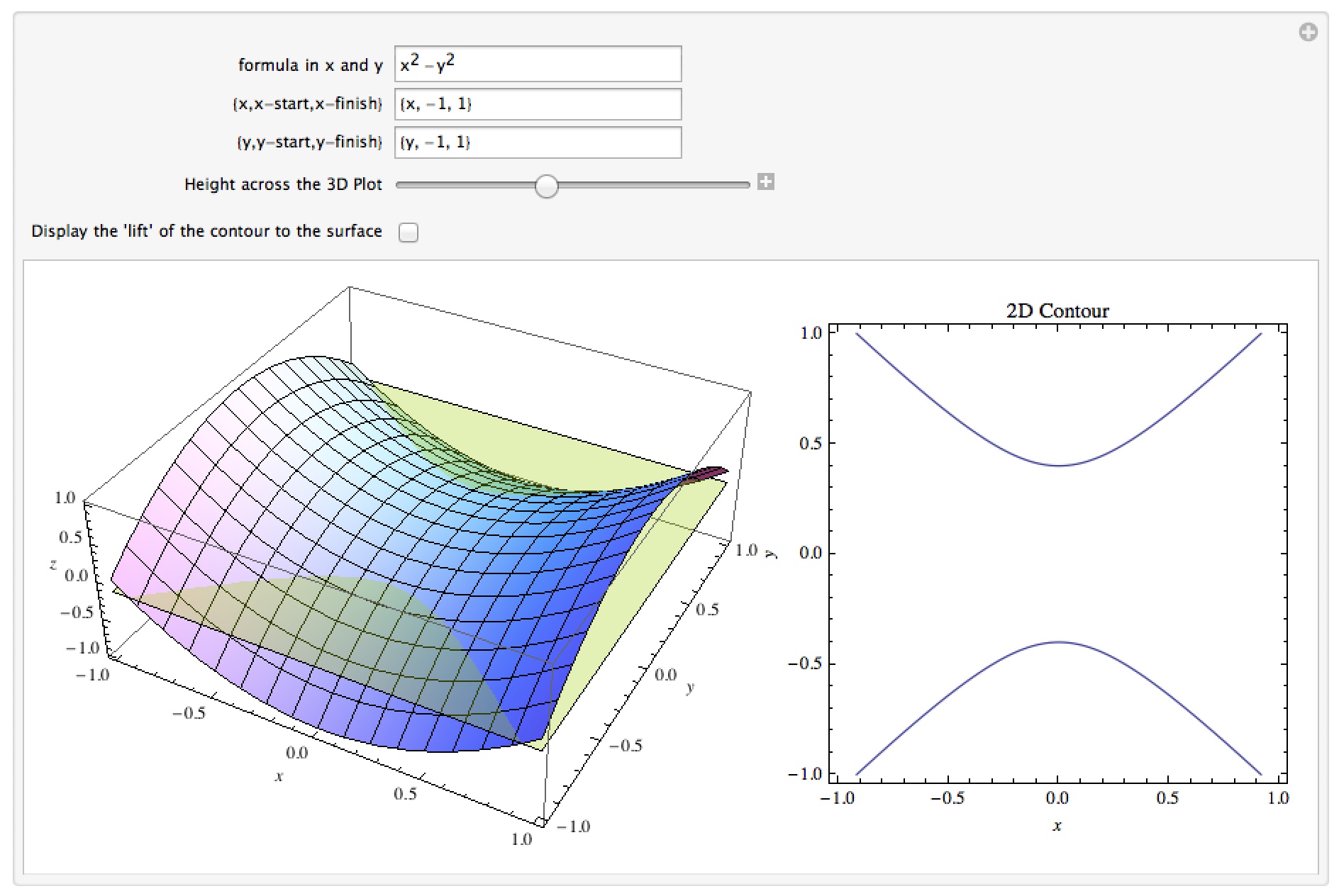



Dr Moretti S Mathematica Notebooks Calculus 3
2, 2 ×Use the keypad given to enter parametric curves Use t as your variable Click on "PLOT" to plot the curves you entered Here are a few examples of what you can enter t 2 − 1 cos ( t) − 2 1 t Here is how you use the buttonsC Graph the level curve AHe, iL=3, and describe the relationship between e and i in this case T 37 Electric potential function The electric potential function for two positive charges, one at H0, 1L with twice the strength as the charge at H0, 1L, is given by fHx, yL= 2 x2 Hy1L2 1 x2 Hy 1L2 a Graph the electric potential using the window @5, 5Dµ@5, 5Dµ@0, 10 D
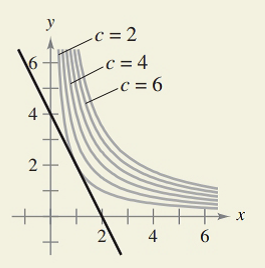



How Do You See It The Graphs Show The Constraint And Several Level Curves Of The Objective Function Use The Graph To Approximate The Indicated Extrema A Maximize Z Xy Constraint
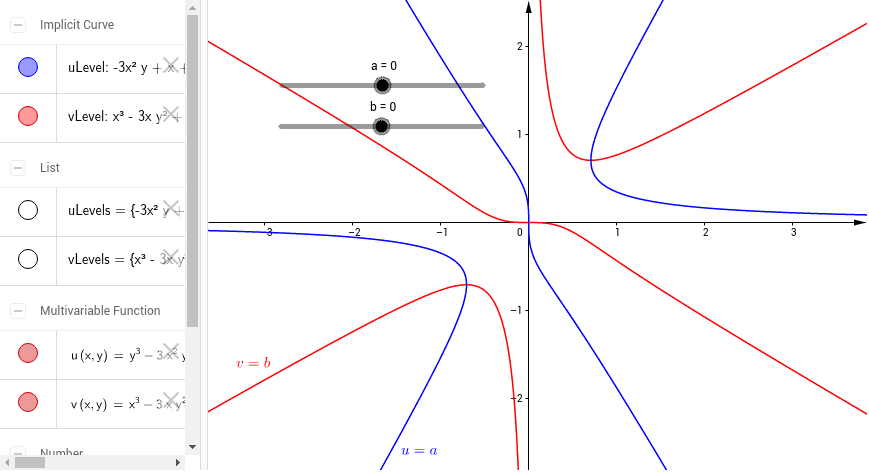



Level Curves Geogebra
Level curves The graph of a function f (x,y) can be studied by drawing level curves f (x,y)=c corresponding to various values of the constant c There is a Maple command that will plot several level curves in the same plot for a given function with evenly spaced values of cLevel Curves and Contour Plots As we've already seen, it is often times very difficult to graph surfaces in $\mathbb{R}^3$ on a flat surface However, we willA free graphing calculator graph function, examine intersection points, find maximum and minimum and much more This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy



Www Usna Edu Users Oceano Raylee Sm223 Ch14 1 Stewart 16 Pdf




Visualizing Gradient Vectors With Level Curves Youtube
5 Plot the level curves by adding a 2D Graph page to the document and plotting the lists as f1(x)and f2(x) Modify the colors of the level curves if desired The examples use the color green for positive values of z, blue for z = 0, and orange for negative values of z 6 Use the Settings Settings dialog to hide the plot labels 7 The level curves of f (x,y) = x 2 y 2 are curves of the form x 2 y 2 =c for different choices of c These are circles of radius square root of c Several of them are shown below One can think of the level curve f (x,y)=c as the horizontal crosssection of the graph at height z=c Plotting 3d graphs and level curves in Matlab I have the following code below, but I cannot test it since I do not have Matlab with me right now and I am afraid I might not have the time to test it by myself when I finally get it I'm trying to plot both 3d graphs and graphs of the level curves in the y and x axis (two dimensions only) of



Level Curves




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware
Level Curves Author Kristen Beck Topic Functions This worksheet illustrates the level curves of a function of two variables You may enter any function which is a polynomial in both andFree online 3D grapher from GeoGebra graph 3D functions, plot surfaces, construct solids and much more!Curves in R2 Graphs vs Level Sets Graphs (y= f(x)) The graph of f R !R is f(x;y) 2R2 jy= f(x)g Example When we say \the curve y= x2," we really mean \The graph of the function f(x) = x2"That is, we mean the set f(x;y) 2R2 jy= x2g Level Sets (F(x;y) = c) The level set of F R2!R at height cis f(x;y) 2R2 jF(x;y) = cg Example When we say \the curve x 2 y = 1," we really mean \The




Finding A Function With Level Curves Mathematics Stack Exchange




Level Curves




Calculus Iii Functions Of Several Variables



Level Sets Ximera




16 1 Functions Of Several Variables




How To Sketch Level Curves Youtube
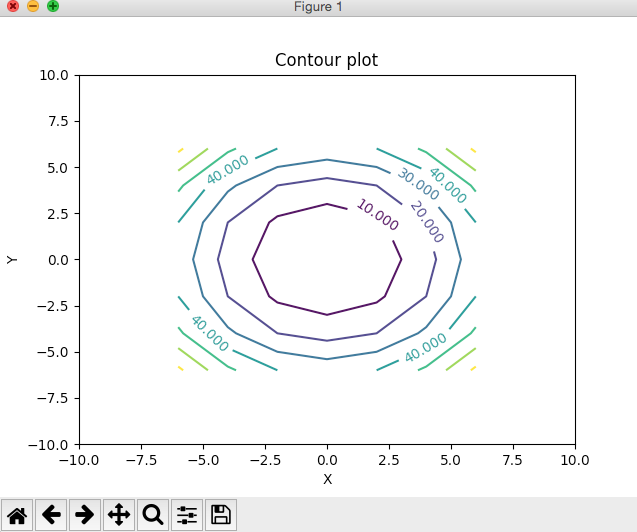



Contour Plot Using Python And Matplotlib Pythontic Com




Graphs And Level Curves




Sketch The Level Curves Of The Function G X Y Chegg Com
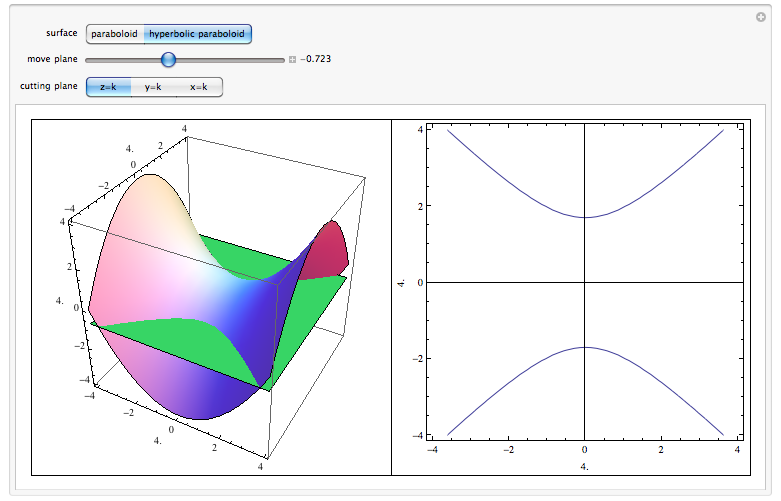



Surfaces And Traces
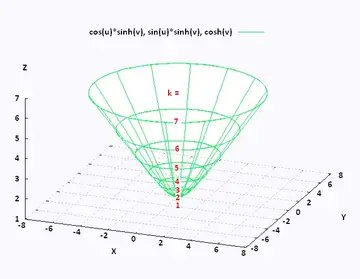



Mathematics Calculus Iii
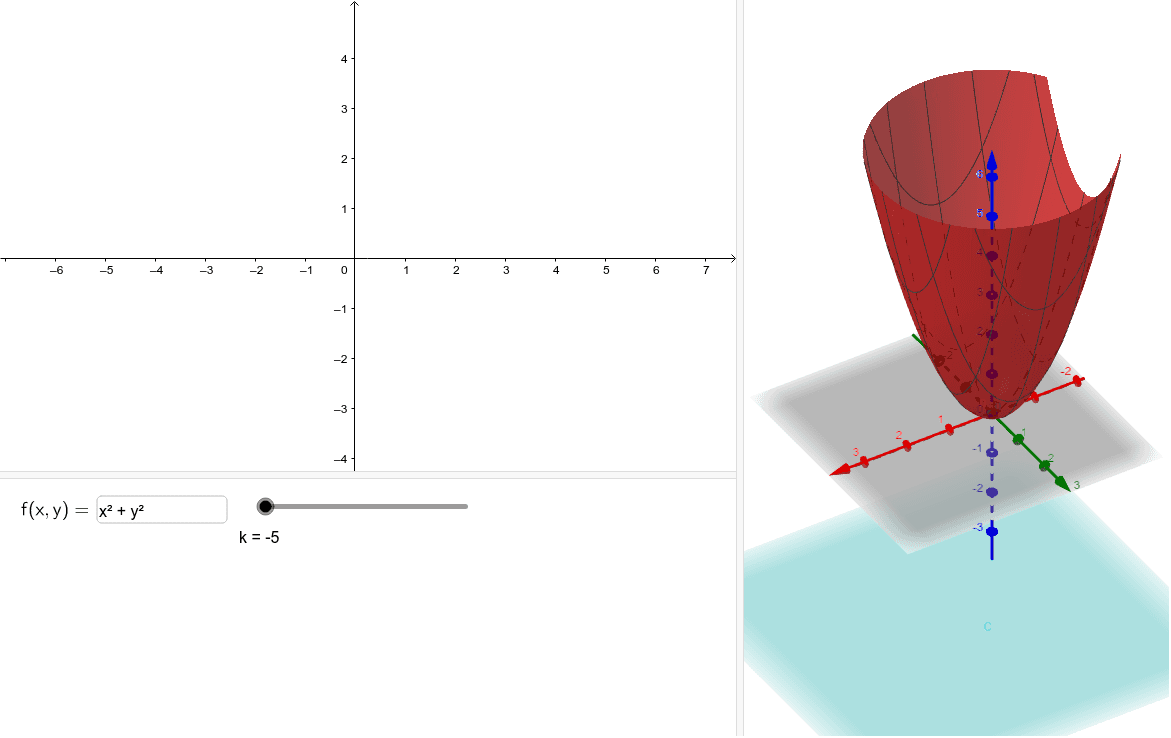



Level Curves Geogebra




Matlab Tutorial




Matlab Tutorial




Level Sets Math Insight




Calculus Iii Functions Of Several Variables




Use A Graph Or Level Curves Or Both To Find The Local Maximum And Minimum Values Homeworklib




Level Set Wikipedia




Level Curves Mit 18 02sc Multivariable Calculus Fall 10 Youtube




Calculus Iii Functions Of Several Variables



Visualizing Level Curves Geogebra




Level Curves




Level Curves Examples Level Surface



Graph A Contour Plots Level Curves Using 3d Calc Plotter Youtube




Describe The Level Curves Of The Function Z X2 Chegg Com



Describe The Graph Of The Function By Computing Some Chegg Com




Level Sets Math Insight
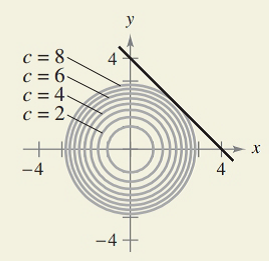



How Do You See It The Graphs Show The Constraint And Several Level Curves Of The Objective Function Use The Graph To Approximate The Indicated Extrema A Maximize Z Xy Constraint



1



12 1 Introduction To Multivariable Functions Mathematics Libretexts




13 1 Day 2 Level Curves Level Curves One Way To Visualize A Function Of Two Variables Is To Use A Scalar Field In Which The Scalar Z F X Y Is Assigned




Graphs And Level Curves



Http Www Personal Psu Edu Sxj937 Math111 Lecture 11 Pdf



Http Www Personal Psu Edu Sxj937 Math111 Lecture 11 Pdf
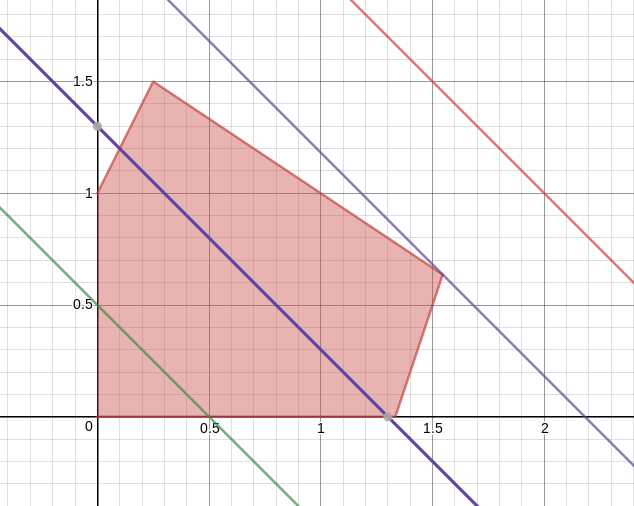



Thinking Of Linear Programs Geometrically




Level Curves Geogebra Dynamic Worksheet



Www Usna Edu Users Math Uhan Sm223 Lessons 12 level curves Pdf
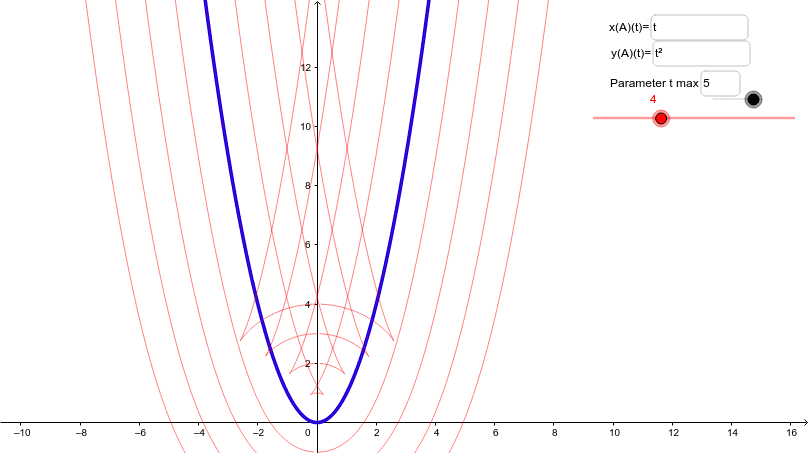



Level Curves Geogebra




14 1 Functions Of Several Variables Mathematics Libretexts




Gradients And Level Curves



Www Arnoldfw Com Pdf Contour Plots Pdf
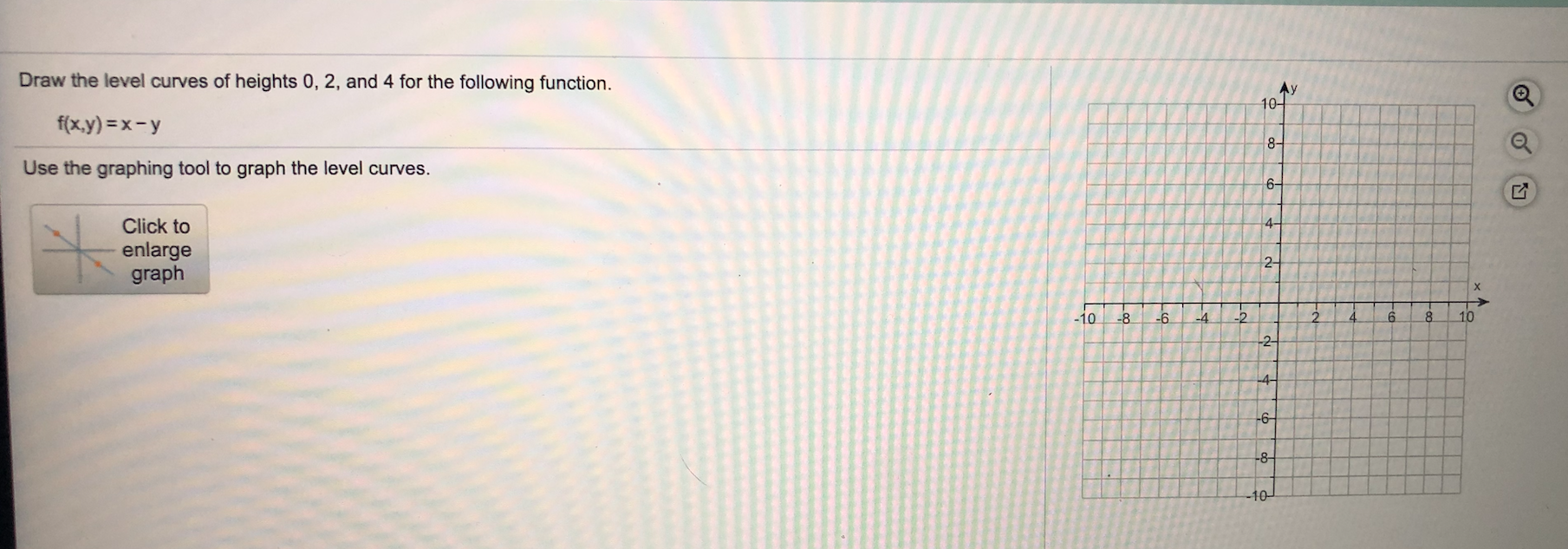



Draw The Level Curves Of Heights 0 2 And 4 For The Chegg Com




14 1 Functions Of Several Variables Mathematics Libretexts




Math 2110 Section 13 1 Level Curves And Level Surfaces Youtube
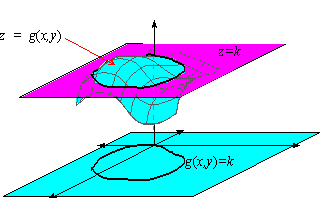



Gradients And Level Curves



Section 13 1 Level Curves Youtube



Tangent Line To A Level Curve Geogebra




Level Sets Math Insight




How Can The Level Curves Of A Quadratic Form Be A Pair Of Lines Mathematics Stack Exchange
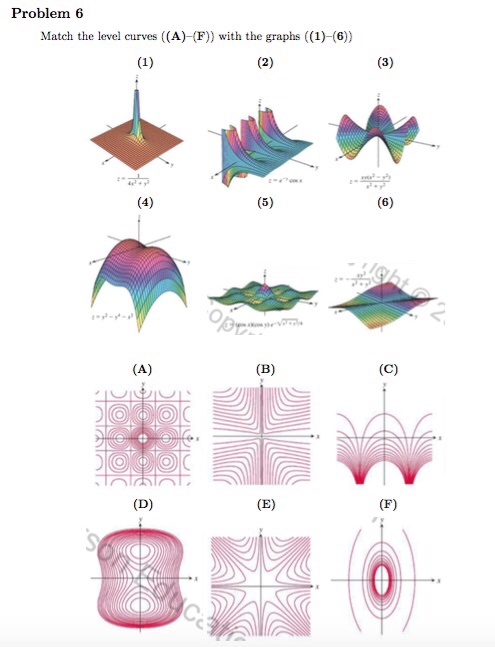



Match The Level Curves A F With The Graphs Chegg Com




Level Set Wikipedia
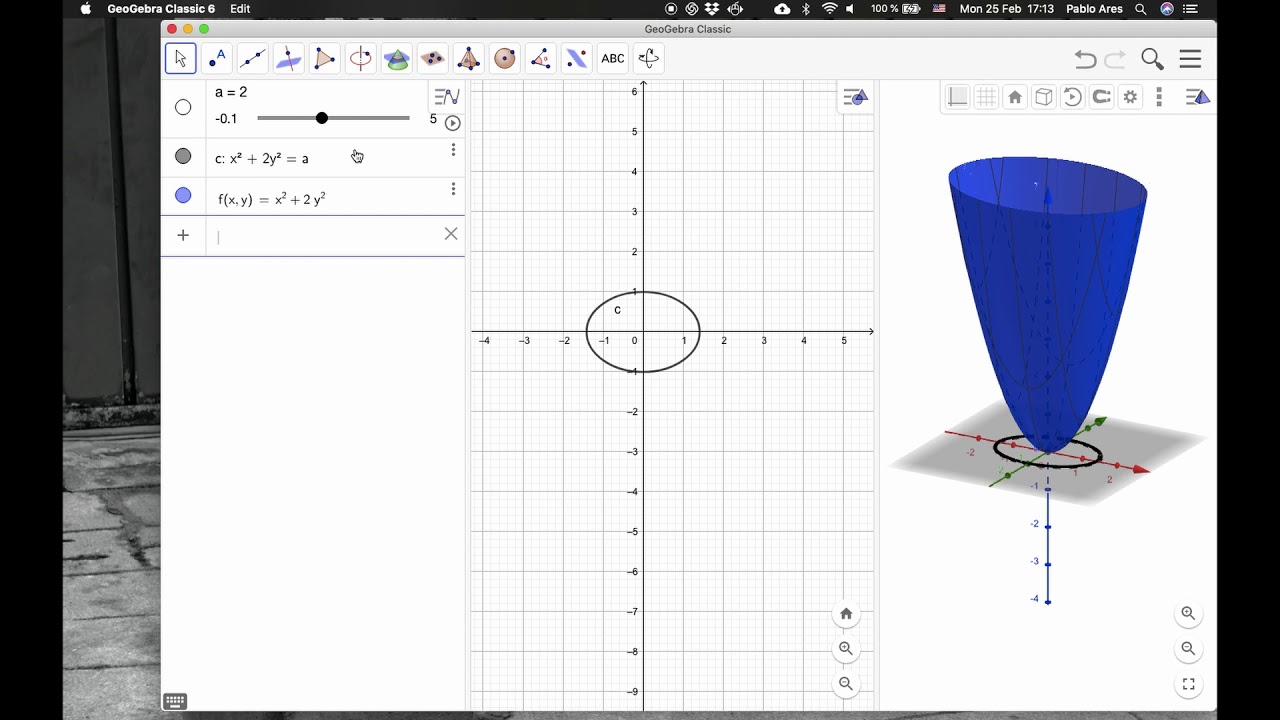



Level Curves Youtube




Level Curves Of Functions Of Two Variables Youtube
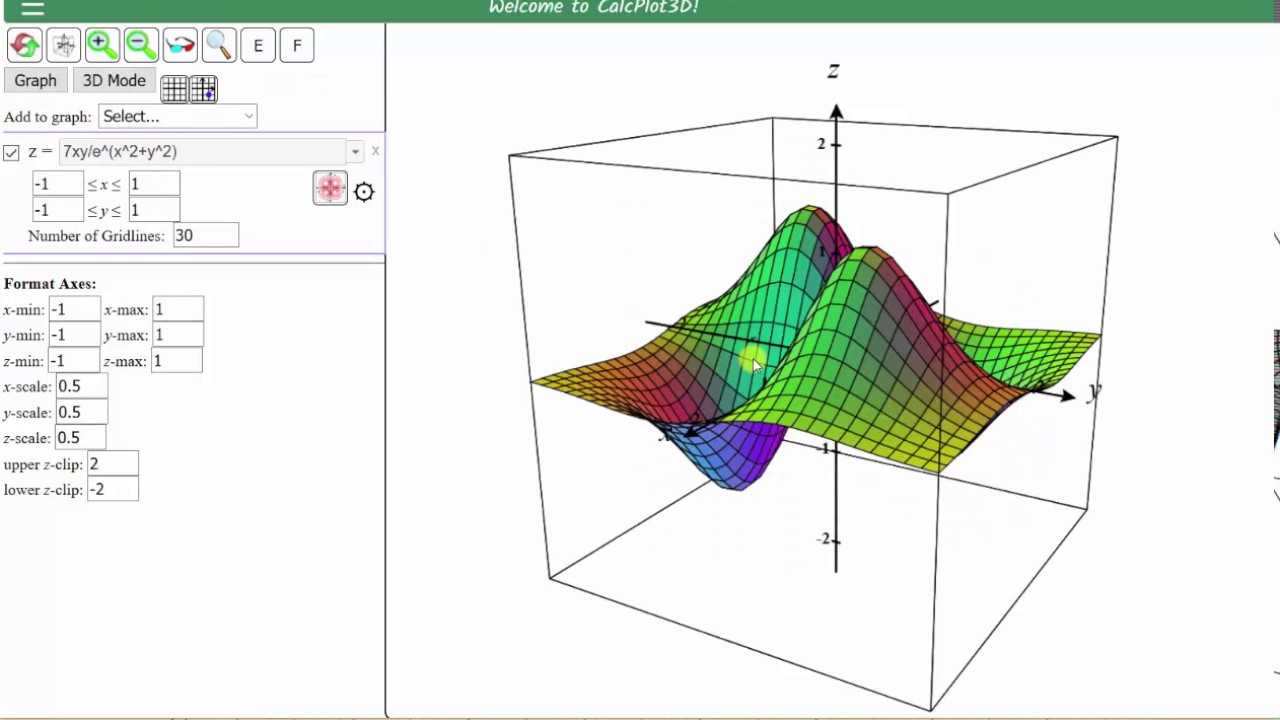



Graph A Contour Plots Level Curves Using 3d Calc Plotter Youtube
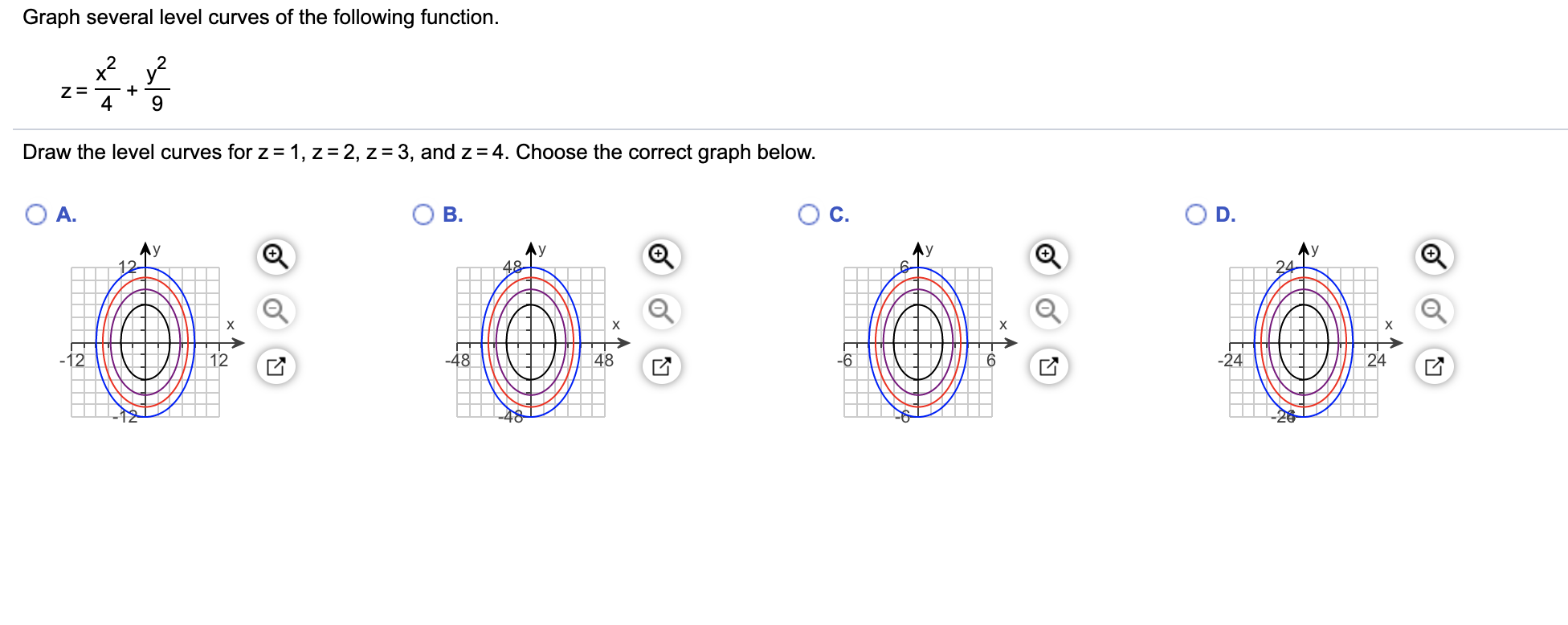



Graph Several Level Curves Of The Following Function Chegg Com
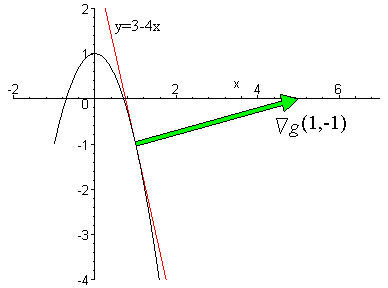



Gradients And Level Curves




Level Surfaces
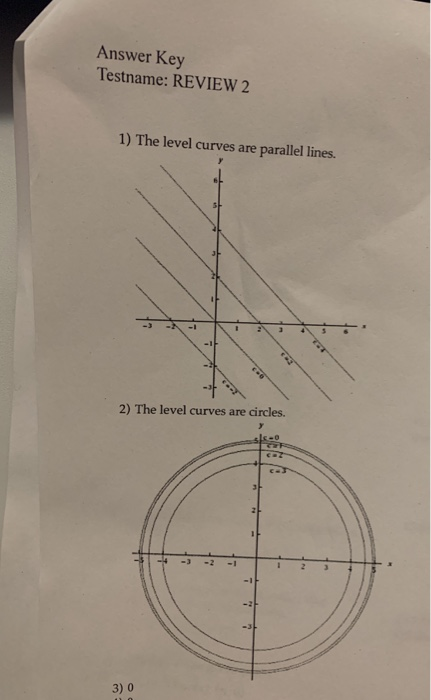



13 1 Describe The Level Curves Of The Function Chegg Com




Session 25 Level Curves And Contour Plots Part A Functions Of Two Variables Tangent Approximation And Optimization 2 Partial Derivatives Multivariable Calculus Mathematics Mit Opencourseware




Level Curves



Level Curves Geogebra



1




Graphing Level Curves Mathematics Stack Exchange




Gradient And Level Curve Geogebra




Level Curves Of Function At Z 0 Mathematics Stack Exchange




What Does It Imply When Two Lines Cross Each Other In A Level Curve Mathematics Stack Exchange
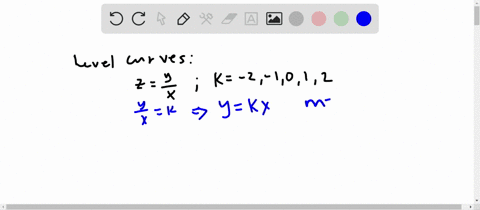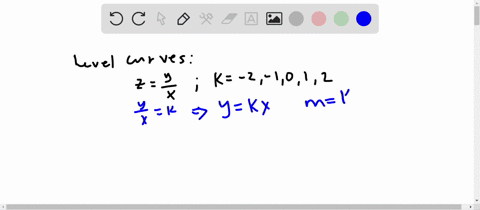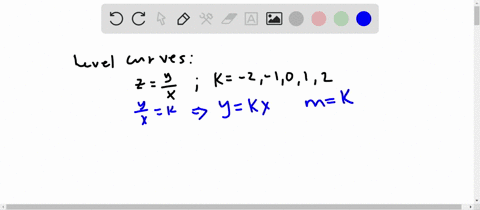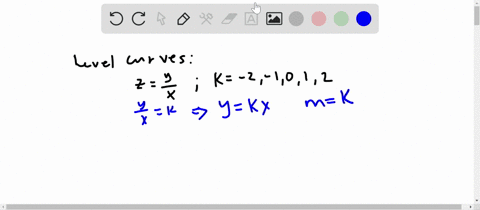



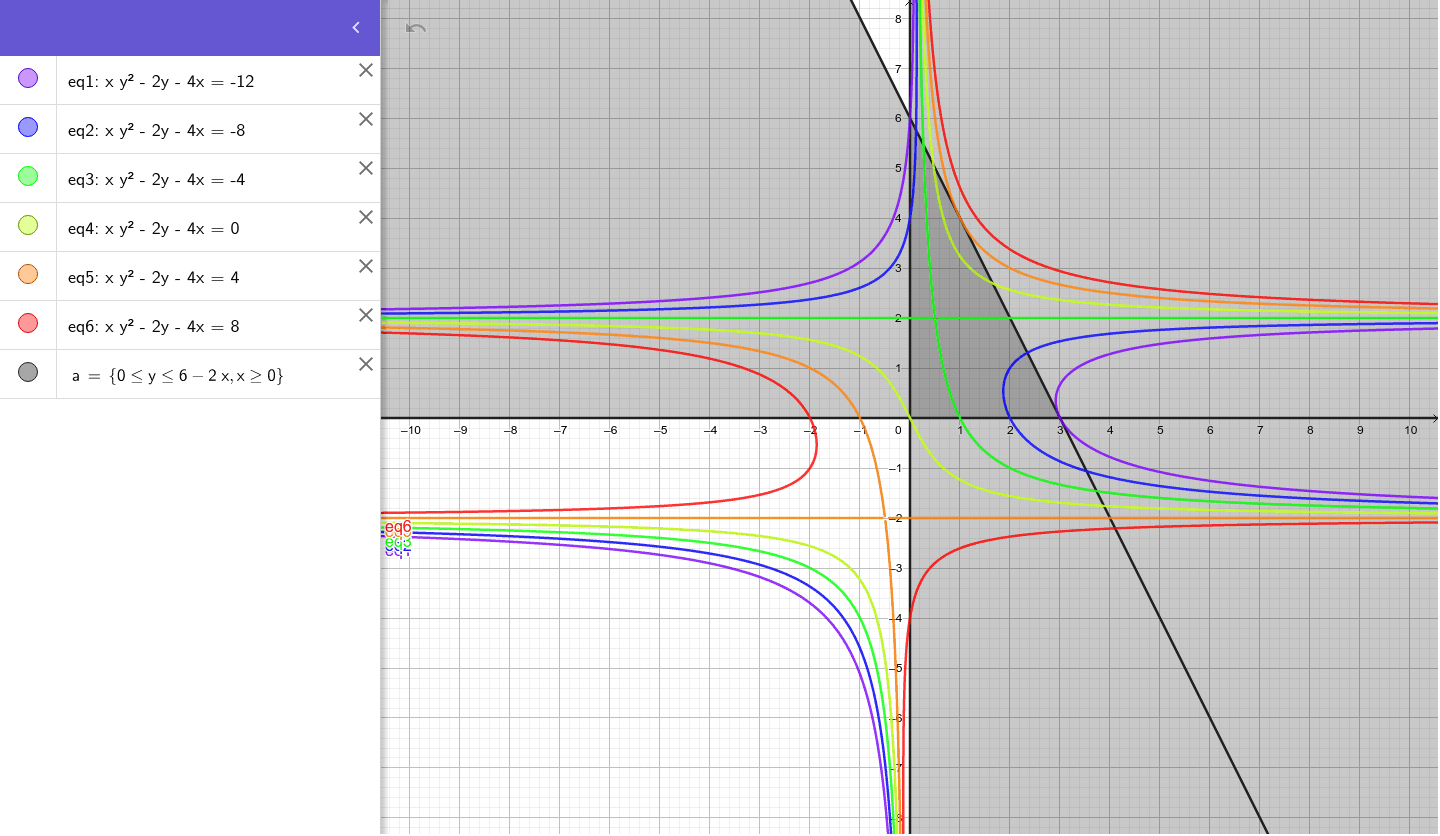
Solved Sketch The Level Curve Z K For The Specifi
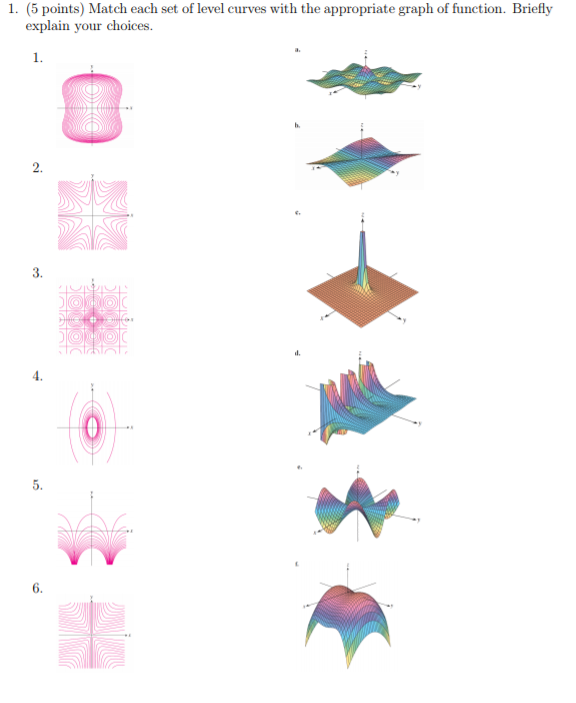



1 5 Points Match Each Set Of Level Curves With The Chegg Com
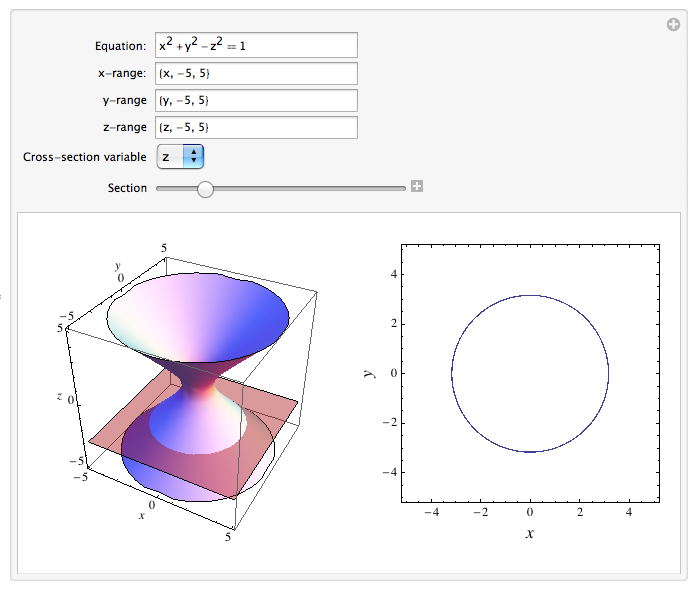



Dr Moretti S Mathematica Notebooks Calculus 3



1




Functions Of Several Variables




Contour Maps In Matlab




Level Set Examples Math Insight




On Your Own Draw Level Curves For The Function F A Chegg Com




Matlab Tutorial




Level Surfaces



Lagrange Multipliers




How Can The Level Curves Of A Quadratic Form Be A Pair Of Lines Mathematics Stack Exchange
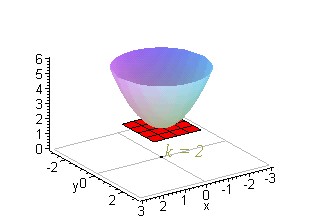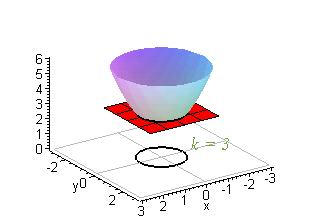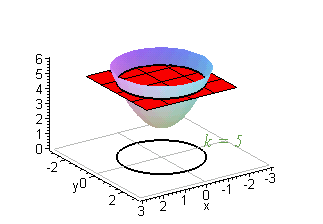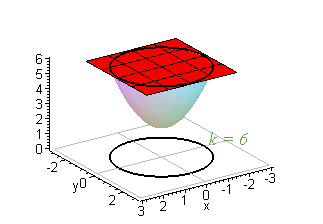



Gradients And Level Curves
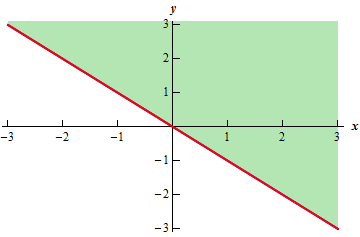



Calculus Iii Functions Of Several Variables



0 件のコメント:
コメントを投稿